一个构件的面相对于另一个构件的面可以自由滑动或分离，就认为两个构件之间存在可变的接触状态非线性，即接触非线性或状态非线性，此时系统的刚度依赖于接触的状态，而接触的分离和接触是一个非线性的过程。
在真实的物体接触过程中两个接触对象是不可能相互穿透的，所以在接触算法方面需要在两个接触对象之间建立一种数学关系来阻止穿透的发生，否则将发生如下图的穿透。
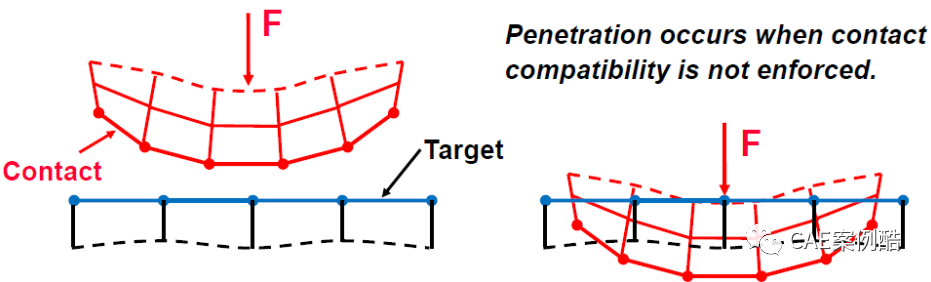
上述阻止穿透建立的关系就是接触算法，在ANSYS中有几种可选的接触算法，他们分别决定了不同的求解接触问题的算法，如下图点开Formulation可以看到所有可选的接触算法。
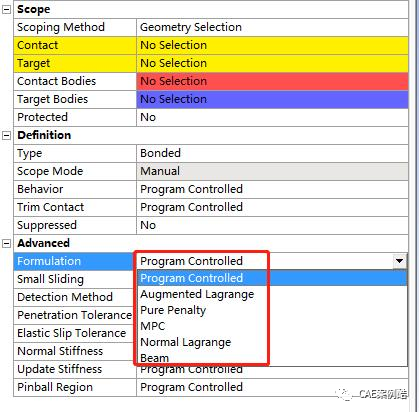
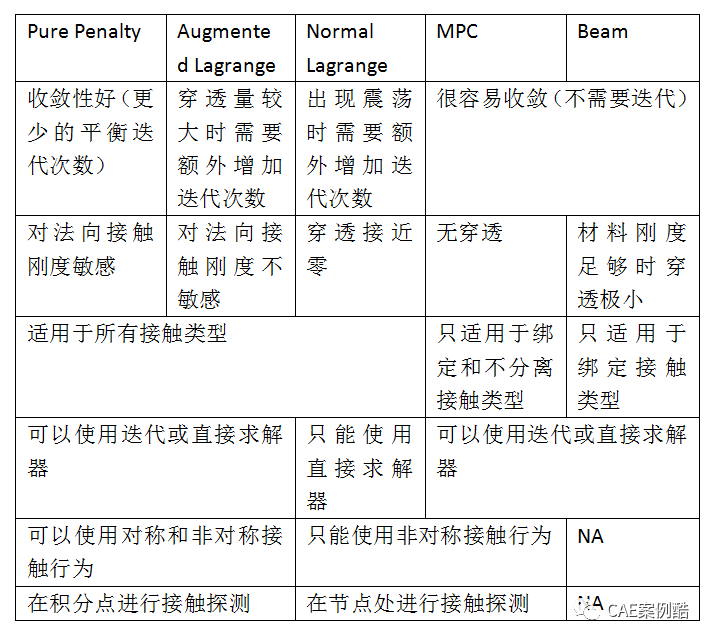
Pure Penalty 和Augmented Lagrange
，这两种接触算法都是基于罚函数法，罚函数法是在接触面之间建立接触力与接触刚度和穿透量之间的关系，接触力等于接触刚度与穿透量的乘积，在算法上零穿透是很难实现的，一般认为微小的穿透可以得到足够精确的解，将三者的关系表达为下式和下图。
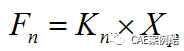
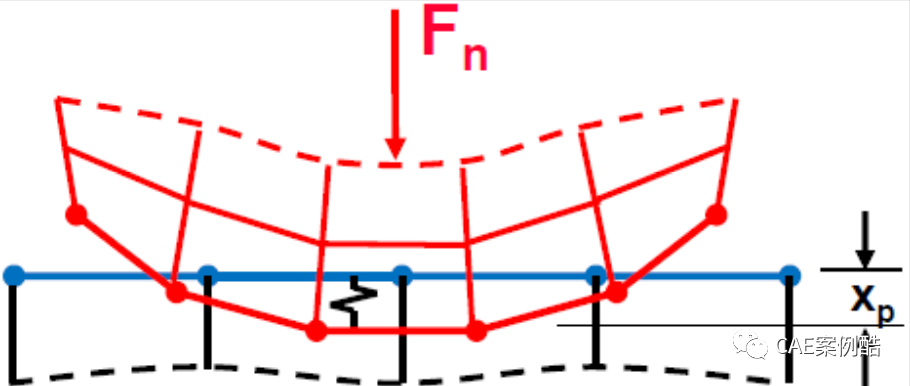
Pure Penalty和Augmented Lagrange之间的区别是Pure Penalty法采用的单纯上式的罚函数，该算法使接触结果对接触刚度的设置比较敏感，而Augmented Lagrange法在纯罚函数算式的基础上增加了额外项，如下式：
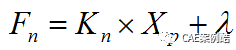
因为额外项以加的形式，所以降低了纯罚函数法对接触刚度敏感的程度。
Normal Lagrange
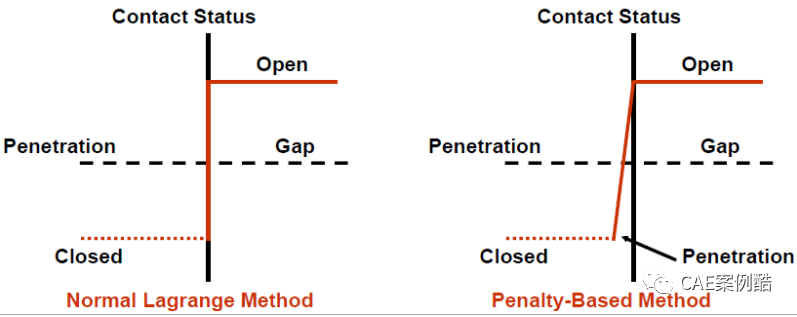
， 该算法增加了“接触压力”作为额外的自由度，这样可以提高接触的适应性，另外该算法直接求解接触压力（作为自由度）而不再像罚函数法那些再去求解接触刚度和穿透量。这样该算法就只呈现两种结果：即要么接触要么分离，存在的问题是在求解过程中极易出现震荡降低收敛性，但是一旦收敛它的精度比较高，因为穿透是零。它与罚函数法的区别可以用下图进行说明，Normal Lagrange算法从Closed状态到Open状态没有过渡的过程，在两个状态的临界状态时容易在两种状态来回跳跃发生震荡。而罚函数法在两个状态之间通过允许小量穿透建立了一个过渡的过程，避免的震荡的发生。
MPC算法
，MPC算法是一种线性接触算法，适用于使用绑定或不分离接触类型时，在接触的两个面之间建立约束方程，该算法适用于大变形的计算场景。
Beam算法
，该算法只适用于绑定接触类型，它是在接触体之间建立无质量的梁单元进行连接。
查看更多评论 >