非线性材料的热疲劳仿真

模拟非线性材料中疲劳的工程师们常常面临着两个挑战。一是必须用正确的本构关系表征材料的力学行为，二是使用一个能够描述寿命控制机制的疲劳模型，应对这两个挑战需要有全面的材料力学知识。今天，我们将讨论在对非线性材料中的热疲劳进行建模时面临的这些挑战。

热疲劳

我们可以使用 COMSOL 软件中提供了一系列预定义的非线性材料模型的 非线性结构材料模块 ，与包含了许多用于不同应用的疲劳模型的 疲劳模块 ，来解决包含上述挑战的一些应用的数值模拟。

当温度变化时，材料会膨胀或收缩。在由几个不同零件组成的应用中，这种热变形将受到限制，因为各种材料的热膨胀系数不同。在存在非线性材料的情况下，这种现象将更具挑战性。

关于非线性材料

材料的非线性意味着变形与载荷不成正比。不同材料的非线性可以大致分为可逆的非线性和不可逆的非线性。可逆的非线性也被称为弹性非线性，这意味着一旦外部载荷回到起始点，应变状态就会回到初始状态。

表现出不可逆非线性的材料在加载时可以承受永久性的损伤，并且在卸载时不会恢复到初始状态。例如，下图中的一个具有非线性焊接材料的 表面贴片电阻 受到了热循环的影响示例就表现出这种现象。

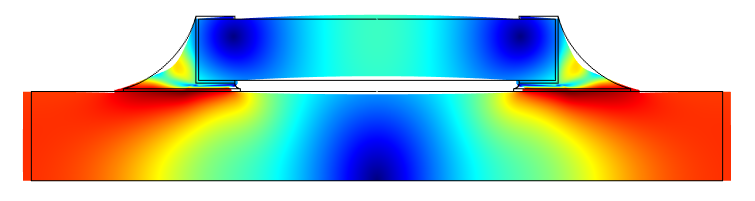
在热负荷周期结束时，表面贴片电阻的位移。蓝色表示零位移。

材料的非线性是一种蠕变机制，一旦材料受到应力场的影响就会发生变形，即使应力场保持不变。由于表面贴片电阻的不同部分的 热膨胀 是不均匀的(底部的印刷电路板更大，顶部的电阻更小)，因此在热载荷循环中，该组件受到了压力。

一旦热载荷达到载荷循环的终点，并返回到初始温度，电阻器两端的焊点就会留下永久变形(蠕变应变)。焊点的永久变形会阻止其余部分恢复到初始状态。我们可以在图中看到这一点，电阻被压缩并隆起，而印刷电路板被拉长。

另一种类型的材料非线性发生在永久变形只取决于施加的载荷，而不是在恒定的应力下变形。这被称为塑性，我们可以简单地通过来回弯曲一个回形针来证明。如果施加的力过大，回形针将保持在不随时间变化的变形状态。塑性和蠕变的结合被称为黏塑性，是另一种非线性材料行为。

稳定的载荷循环

反复的加载和卸载会引起疲劳裂纹。在评估疲劳寿命之前，必须获得一个稳定的载荷循环。在处理非线性材料时，在材料的响应趋于稳定之前，往往需要许多载荷循环。一般来说，非线性材料对循环载荷的反应可以用三种情况来概括：立即稳定、安定和棘轮。

• 在立即稳定 的情况下，第二个载荷循环已经给出一个稳定的应力-应变响应，可以代表每个连续的载荷循环。下图中案例(a)的黑色虚线证明了这一点。
• 在安定 的情况下，伸长在一定数量的循环后首先停止。因此，可能需要对大量的循环进行模拟。详见案例(b)。
• 在棘轮运动中，如案例(c)所示，材料经历了持续的伸长，直到失效。从疲劳的角度来看，这种情况是最具挑战性的，因为永远不会得到一个稳定的负载荷循环。在这种情况下，通常必须模拟从初始状态到失效的所有周期。

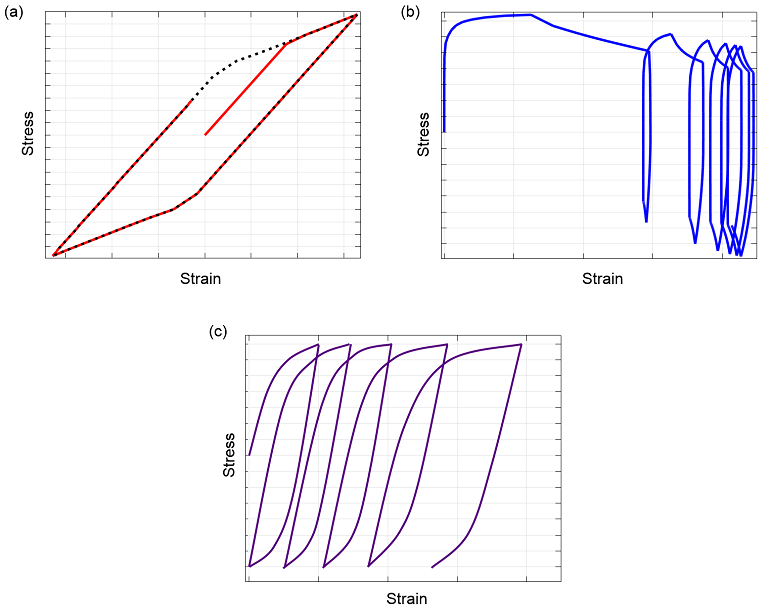
材料对重复载荷循环的响应：(a)立即稳定(b)安定和(c)棘轮。

非线性材料的疲劳模型

没有一个通用的模型可以预测所有非线性材料的疲劳，长久以来，人们提出了许多模型。在 20 世纪 50 年代，Coffin 和 Manson 研究了金属的疲劳，并提出了疲劳寿命和低周期疲劳状态的塑性应变之间的指数关系。

在这项开创性的工作之后，许多研究人员对这个模型做了稍微的修改，其中塑性应变被其他不同的应变类型所取代，如蠕变应变、塑性剪切应变、总剪切应变，以及其他。下面，你可以看到两个应变类型(有效蠕变应变和剪切蠕变应变)在一个 表面贴片电阻模型 中的比较，这个模型来自 COMSOL 案例库。

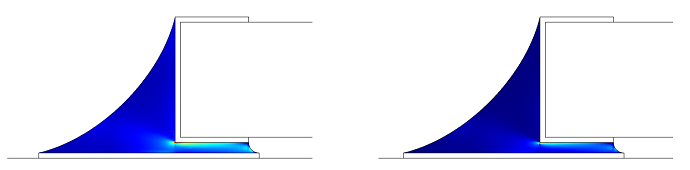
焊点中的蠕变应变的发展。左边是有效蠕变应变，右边是剪切蠕变应变。

可以看到，这两种应变测量在焊料和电阻的界面上都是最高的，这与实际应用中热疲劳裂纹的位置相吻合。

对于许多应用来说，仅仅依靠应变是不足以进行疲劳预测的。相反，能量可能更适合，因为它结合了应力和应变的效果。20 世纪 60 年代，Morrow 提出了疲劳寿命和循环塑性应变能量之间的指数关系。这个模型后来被修改为取决于其他能量变量，如蠕变应变能、总应变能、应力-应变滞后能、黏塑性应变能等。

很多时候，控制疲劳的能量变量是一个非标准的能量变量，需要单独评估。这可以在 COMSOL Multiphysics 中完成，如 加速寿命试验 的例子所示，非线性材料有两种蠕变机制。第一个机制控制低应力下的应变，第二个机制控制高应力下的应变。另一方面，疲劳仅由高应力下的蠕变发展引起的能量耗散来控制。

应变发展以及不同机制的能量耗散是在单个分布式常微分方程接口中评估的。

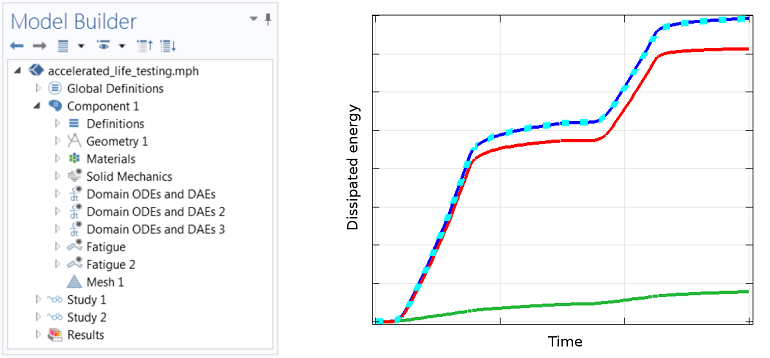使用常微分方程接口评估用户定义的蠕变应变和能量的模型设置(左侧)。用户定义的本构关系与非线性结构材料模块中预定义的材料模型之间的结果比较(右侧)。绿线是低应力下的耗散能量，红线是高应力下的耗散能量，绿松石色的虚线是两种机制的综合耗散，蓝线是用非线性结构材料模块的材料模型评估的耗散能量。

疲劳裂纹经常出现在几何形状急剧变化的边界和角落里。这些地方也是众所周知的造成数值奇异的地方。因此，在那里进行点评估会产生误导性的结果。

Darveaux 提出了一个使用能量体积平均值的模型。这种方法减少了对关键地方的网格划分的敏感性，并根据周围的状态来预测疲劳寿命。在下图中，我们使用 Darveaux 模型，根据球状网格阵列中耗散的黏塑性应变能量来预测疲劳寿命。

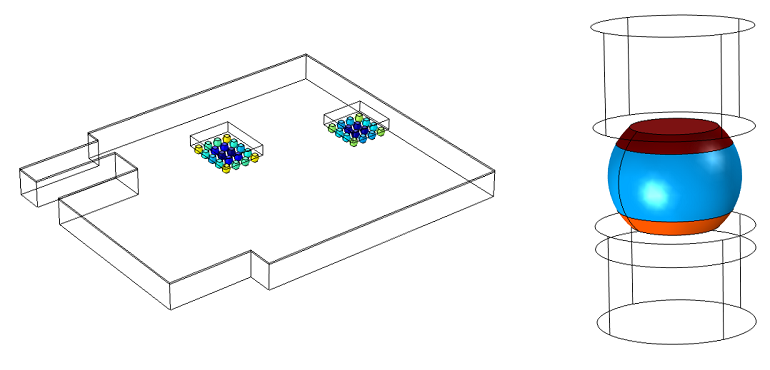
基于平均耗散的蠕变能量的疲劳寿命。在左边的完整模型中分析了两个球栅阵列中的所有接头，在右边的子模型中显示了对关键焊点的详细研究。

首先，对所有焊点进行分析，以确定关键焊点。然后，在一个详细的研究中，使用 前一篇文章中描述的子模型技术 对临界焊点进行重新分析。最后预测在与其他材料交接处的薄层的疲劳寿命，预计此处会出现裂纹。由于该模型评估的是体积平均值，所以结果是按域评估的。

我们可以在基于应变的疲劳功能中用不同的应变选项评估 Coffin-Manson 模型。Morrow 和 Darveaux 模型具有不同的能量选项，可以使用基于能量的疲劳功能进行评估。

热疲劳建模示例

作为总结，我们分享官网中几个模拟非线性材料的热疲劳的例子。

• 表面贴片电阻器的热疲劳模型 演示了如何使用 Coffin-Manson 和 Morrow 类型的关系，根据蠕变应变和耗散的蠕变能量来进行疲劳评估。
• 球栅阵列中基于能量的热疲劳预测 示例中，分析了一个包含几个黏性焊点的微电子芯片。疲劳寿命是基于 Darveaux 能量体积平均值所的评估的。这个模型也展示了 如何使用子模型的概念来分析大型模型 。
• 加速寿命测试 示例中模拟的疲劳寿命预测，是基于更奇特的能量和应变表示。在这个例子里，评估了一个具有两种蠕变机制的材料行为，预测了基于一种机制的疲劳寿命。两个机制中的应变分离需要使用单独的常微分方程接口重新评估单个应变。

本文来自 ：COMSOL 博客