分析真实条件下的设计往往需要考虑几个相互作用的物理现象,如非等温流动或热膨胀。然而,并不总是需要包括两个方向的相互作用(例如,对流热传递和流场的温度依赖性),可以考虑单向耦合。这样做可能会大大降低计算成本,而对求解精度的影响可以忽略不计。这篇文章我们将展示在 COMSOL Multiphysics® 中考虑单向耦合的优势。
单向耦合方法的优势
在运行多物理场仿真时,如果一个物理过程对另一个物理过程的影响与求解的精度要求相比可以忽略不计,那么就可以节省大量的计算时间。在这种情况下,我们可以在第一个研究步骤中对一个物理场接口进行计算,然后将结果作为第二个研究步骤中求解的第二个物理场几口的输入,这在 COMSOL Multiphysics 中是很容易做到的。
以非等温流动为例,我们首先计算流场,并将其作为传热问题的输入。我们不是求解一个双向耦合问题(流动 ↔ 传热),而是求解一个更简单的单向耦合问题(流动→传热)。如果流场的解可以多次重复使用,那么计算时间和内存的减少甚至更高;例如,当对同一流场进行不同传热条件的参数化研究时。
单向耦合方法可以应用于所有类型的流体流动,包括湍流状态和多孔介质中的流动。只要耦合较弱,也可以将这种技术应用于任何平流场;例如,稀溶液中的化学物质传输。
还有一些其他的多物理场耦合的情况,这种方法也适用;例如,传热和结构力学之间的耦合引起的热膨胀。在这种情况下,我们可以先计算温度场,并将它作为力学分析的输入,前提是变形对温度场的影响可以忽略不计。
单向耦合方法有效性的重要标准是,第二个计算的物理现象对第一个计算的物理现象的影响远远小于分析所需的精度。例如对于非等温流动,我们必须检查由温度变化引起的密度和黏度的变化是否足够小,以使它们对流场的影响落在分析的精度限制之内。建议在单向耦合的情况下,将流动的平均温度作为密度和黏度的参考温度。
检查单向耦合方法有效性的最好方法是求解一个测试问题,并将结果与同一问题的双向耦合解进行比较。在分析中选取几个计算完全耦合问题的样本点,将简化方法与完全解进行验证。如果这些点在要求的精度范围内,我们就可以使用简化方法进行大部分的计算。我们需要明智地选择样本,因为验证点必须落在运行的模拟窗口内。理想情况下,这些点应该是极端条件,所有其他计算都应该落在极端点内。
如果事实证明单向耦合对某一模拟任务来说不是一个合适的简化,使用这种技术仍然是有帮助的。首先求解解耦问题的方法是一个很好的选择,可以为完全耦合的问题获得良好的初始猜测;例如,对于稳定的非等温流。有些情况下,除非提供一个合适的初始猜测,否则流场不会收敛,这就是我们用文中讨论的方法可以得到的。
用单向耦合对压力容器中随温度变化的塑性进行建模
COMSOL 案例库中的压力容器中温度相关的塑性模型是两个物理现象有效单向耦合的一个很好的例子。
一个承受快速温度变化的压力容器。冷却过程中的温度梯度导致不锈钢覆层的塑性变形,其中屈服应力和硬化函数取决于温度。与其同时计算随时间变化的温度场和产生的塑性变形,不如将问题分成三个独立的研究。
-
初始化步骤,由容器内外的温度和压力条件,可以得到初始应力和温度分布。
-
对突然通过管道流入容器的冷水引起的温度发展进行瞬态分析
-
使用所得到的瞬态温度场来计算弹塑性变形的发展,来进行一系列稳态研究步骤
-
我们可以利用这样一个事实,那就是变形不影响温度场。(题外话:物理上可能存在一个非常小的这种影响,但为了描述它,流体和结构之间的热传递必须使用完整的流体-结构分析来计算,而不是使用对流条件来指定。)
-
变形可以被看作是与时间尺度有关的瞬时的,这就是为什么在每个时间点都有一个力学分析的稳态解。
为了建立这个相当复杂的序列,只需要从以前的研究步骤中选择正确的初始条件,并定义一个时间参数 t,它被用作最后参数化稳态研究的占位符。变形是使用传热研究中相应时间点的数值自动计算的。
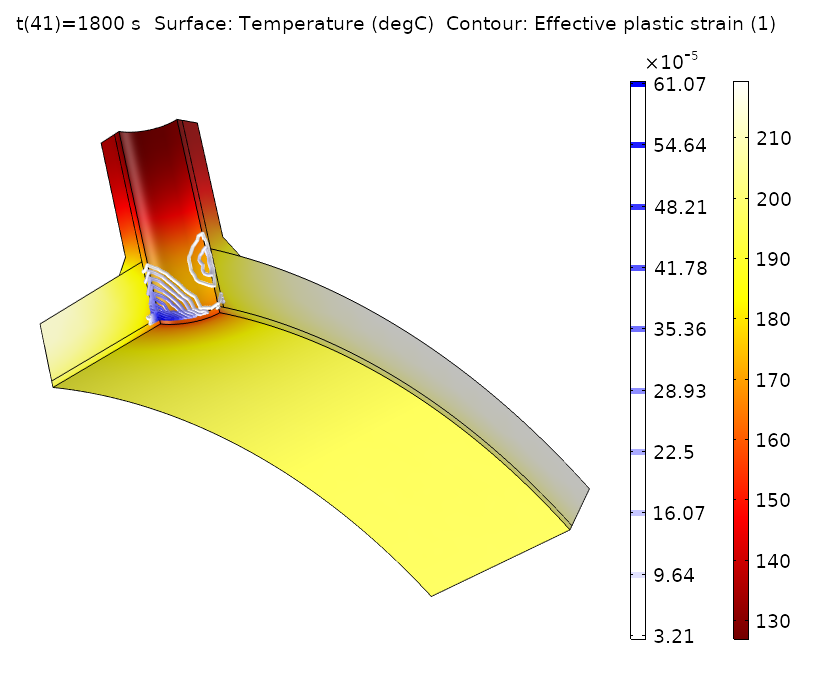
大幅降温后压力容器的温度场和有效塑性应变。
单向耦合的错流式换热器建模
我们用一个非等温流的例子错流式热交换器教程模型来尝试一下单向耦合的方法。这种类型的热交换器在生物技术中的片上实验室装置和微型反应器中都可以找到,例如用于微型燃料电池。
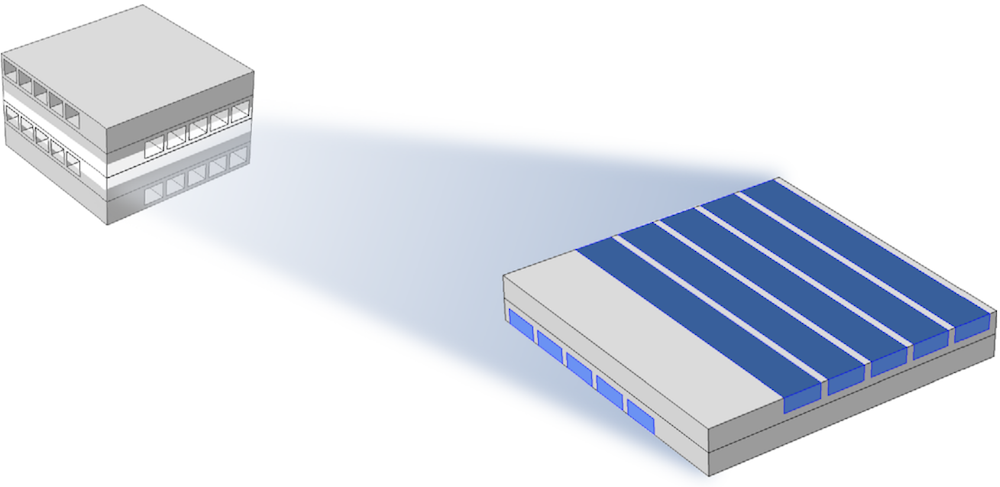
微型热交换器的模拟部分。
如上图所示,建模系统包括两组通道,一热一冷,以交错流动的方式排列,每组有五个通道。由于热交换器具有对称性,该模型被缩小。
如果检查模型的研究节点,我们会发现有两个固定的研究步骤。在第一个研究步骤中,只选择层流(spf)进行求解,而在第二个研究步骤中,同时选择了传热(ht)与多物理场耦合非等温流(nitf1)。在第一个研究步骤中对流场进行求解,由于非等温流动 多物理场节点提供的应用耦合,在第二步骤中可以自动得到结果。这种研究设置从 COMSOL Multiphysics 5.3 版本开始预设并且可用,在稳态模拟中称为稳态,单向耦合,非等温流动(NITF),在瞬态模拟中称为瞬态,单向耦合,非等温流动(NITF)。
单向和双向耦合的结果比较
我们可以通过增加一个稳态的、完全耦合的研究步骤的新研究,来比较单向耦合方法和双向耦合方法的结果。在计算了这两个研究后,发现结果只有微小的差别。上部通道壁上的平均传热系数,可能是模型最感兴趣的结果,在双向耦合中为 3147.7 W/(m2K),在单向耦合中为 3147,5 W/(m2K)。0.2 的差异可能比两次计算的数值误差小得多。此外,计算时间也减少了一半,从双向耦合问题的约 83s 到单向耦合问题的30s。
这两种方法的综合比较可以在模型文件中的幻灯片演示中找到。
双向耦合稳态解的温度结果。
如果对模型的瞬态行为感兴趣,还可以进行其他研究组合。例如,我们可以增加两个瞬态的研究步骤,首先解决流动问题,然后是瞬态传热研究步骤(瞬态,单向耦合,非等温流动)。如果流动条件不随时间变化(温度除外),我们也可以创建一个具有稳态流动和瞬态传热研究的研究序列。下表概述了不同的研究组合和它们各自的计算时间,模拟时间为 10s。
不同研究方法在 Intel® Xeon® W-2135 @ 3.70 GHz 机器上的计算时间。
正如预期的那样,在瞬态传热与稳态流场单向耦合的情况下,计算速度更快。就计算时间而言,我们所示例的问题显然很小,但随着问题的增加,文章中讨论的简化方法就会成为一个更重要的选择。
文章来自:COMSOL博客

 当前暂无评论,小编等你评论哦!
当前暂无评论,小编等你评论哦!



















