上一期讲过“为什么复合材料层压板设计中经常要求均衡性？”，主要是避免由于非均衡性引起的拉剪、剪拉、弯扭、扭弯耦合效应。今天再简单讲一下“为什么复合材料层压板设计中又经常要求对称性？”
航空航天领域常用的π/4层压板（由0°、90°、45°、-45°四种铺层角度组成的层压板）设计中，经常会提到对称性设计约束条件。对称性就是铺层序列中同材料、同角度的铺层对称分布在中性面两侧。
例如：
[0/90]s：下标s表示对称，实际铺层顺序为[0/90/90/0]。
图1 对称铺层示意
为什么要保持对称性的约束条件，同样需要从最基本的复合材料力学原理去解释。上一节曾经描述过，对于单向层合板，在材料坐标系下的应力应变关系如下，其中Q为弹性矩阵：
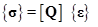
或
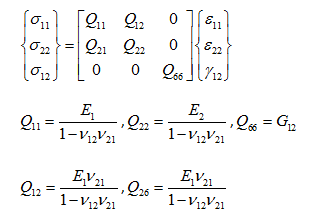
对于一个包含多个铺层角度的
层压板
，其第k个铺层，在层合板坐标系下单层的应力应变关系为：
其中，
Q'为偏轴弹性矩阵，由
Q通过矩阵变换得到。
θ为铺层角度。这里需要注意的是，偏轴弹性矩阵系数Q
11'、Q
22'、Q
66'、Q
12'四项均为
偶函数，+θ和-θ两个铺层对应的偏轴弹性系数相同，比如Q
11'(+θ)=Q
11'(-θ)。而Q
16'和Q
26'两项是
奇函数，+θ和-θ两个铺层对应的这两个偏轴弹性系数刚好
大小相等，符号相反，例如Q
16'(+θ)=-Q
16'(-θ)。
在讲均衡性的时候重点看的是A16、A26、D16、D26。本期重点看一下耦合刚度矩阵B.
根据上式中B矩阵的表达式，当相同材料、相同铺层角度的两个铺层对称分布在层压板中性面两侧时，相同材料保证了Q阵的一致，相同铺层角度保证了Q'矩阵的一致。假定层压板中一共有N个铺层，第k铺层与第N-k层对称，如下图所示。两个对称铺层，无论角度是多少，其累加之后的B矩阵都是0。
图2 层板厚度方向几何分层示意图
图3 B矩阵为0
B矩阵为0，表示面内的拉伸、压缩、剪切变形不会诱导出面外的弯曲、扭转变形，即不存在面内-面外、面外-面内耦合。
反之，如果一个层压板中铺层不对称时，B矩阵不为0，面内
拉伸、压缩、剪切
变
形会引起面外的弯矩、扭矩，层压板也必然产生附加的面外弯曲或扭转变形，即存在
拉伸-弯曲、拉伸-扭转、剪切-弯曲、剪切扭转耦合效应。同样滴，也会存在
弯曲-拉伸、扭转-
拉伸、弯曲-剪切、扭转-剪切
耦合效应。
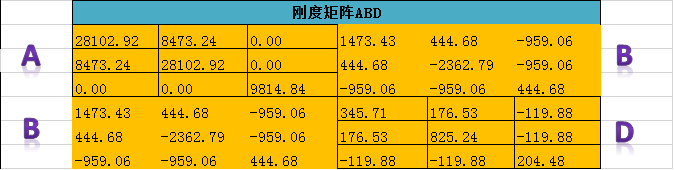
图4 B矩阵非0
回到开头的问题，“为什么复合材料层压板设计中又经常要求对称性？”，主要是避免层压板的面内-面外、面外-面内
耦合效应
，这类耦合效应会导致层压板成型阶段较大的翘曲变形以及加载过程中出现附加的非期望变形。
最后提醒大家需要注意的是，对称性与上一节讲述的均衡性不同，非
均
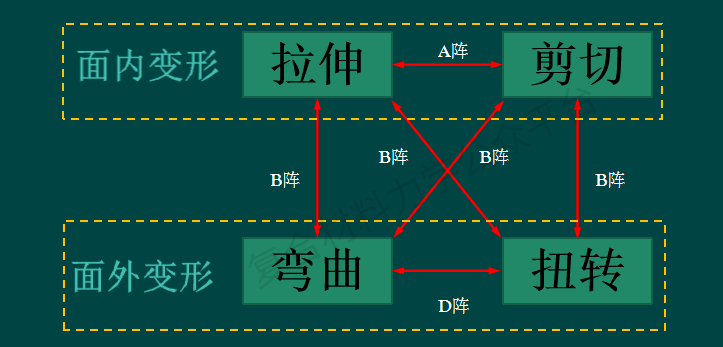
衡性引发的是面内-面内（A16、A26主导）
、面外-
面
外（D16、D26主导）的耦合，而非对称性引发的是面内-面外、面外-面内的耦合(B矩阵主导)，如下图所示
。
当前暂无评论，小编等你评论哦！
