聚合物材料模拟：概述和实例

引言

聚合物材料具有从纳米到微米空间尺度的多尺度性质，因此有必要仔细考虑现象和物理性能的起源尺度。尽管通过实验和测量技术的发展已经阐明了许多机制，但模拟技术在仅依靠这些方法无法捕捉的领域中发挥着重要作用。此外，模拟技术还在使用数据科学预测物理性能方面的最近进展中发挥着互补作用。

在下文中，我们将介绍一些聚合物的代表性模拟技术、它们的合作、软件等。这些方法按照空间尺度从最小的顺序描述，因为如果关注每种方法针对的空间尺度，将更容易理解。

1、量子化学 & 密度泛函理论

该方法主要针对几纳米或更小的尺度，基于薛定谔方程计算分子和晶体中的电子态。它尤其用于评估材料的电子性质，如激发、极化、分子间力和化学反应。有分子轨道方法（MO）和密度泛函理论（DFT），可以通过将电子密度作为计算目标来减少计算负担。这些方法中的每一种都根据如何纳入电子相关性、如何选择基函数等进行细分。

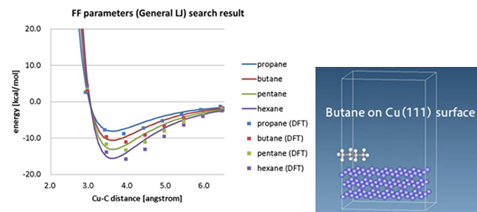
图1. 通过DFT评估分子在铜表面的吸附能

（左图：丙烷/丁烷/戊烷/己烷分子的吸附能曲线；右图：计算模型）

图1显示了在考虑范德华力的情况下，分子吸附在铜晶体表面时，距离表面的距离与能量之间的关系的DFT计算结果（每种分子种类用点表示），以及拟合到用于分子动力学的Lennard-Jones（LJ）势的曲线。表面吸附能在界面设计中非常重要，但在某些情况下，没有合理的LJ势参数，需要通过DFT或其他方法进行评估。

2、全原子分子动力学

在全原子分子动力学（FAMD）中，一个粒子代表一个原子（图2左），每个粒子的动力学是基于牛顿运动方程计算的。作用在每个原子上的力由一个函数和参数给出，包括上述的LJ势。FAMD可以用来评估分子结构变化（如官能团）对分子构象和动力学的影响。例如，聚合物在体积状态下的密度和弹性模量，其中气体分子的自由体积分布和扩散以及有向（晶体）结构。由于其适用于各种应用，FAMD变得很受欢迎。另一方面，只要使用通用计算机，可以处理的空间尺度约为10纳米，时间尺度在使用最近的软件和硬件（如GPU）时为100纳秒量级。这对于处理聚合物的长时间松弛现象等是不够的。

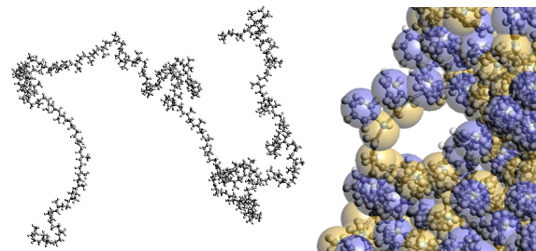
图2. 左图：FAMD表示的聚异戊二烯分子结构，右图：CGMD图像

3、粗粒度分子动力学

在粗粒度分子动力学（CGMD）中，一个粒子代表几个原子的一组（图2，右）。例如，在评估橡胶材料的拉伸性能时，需要在可以处理橡胶状态的时间尺度（变形速率）上进行计算。这很难通过FAMD实现，但可以通过CGMD实现。粗粒度单元之间的相互作用（粗粒度势）可以基于FAMD确定。或者，可以使用简化参数进行计算，然后与实验数据（如MPa等单位）进行交叉验证。

在图3中，评估了由三嵌段共聚物（如苯乙烯-异戊二烯-苯乙烯（SIS））形成的相分离结构（热塑性弹性体）在单轴拉伸过程中的行为。下文描述的平均场方法计算结果用于构建初始结构。在拉伸过程中捕捉了领域和分子链的变形。

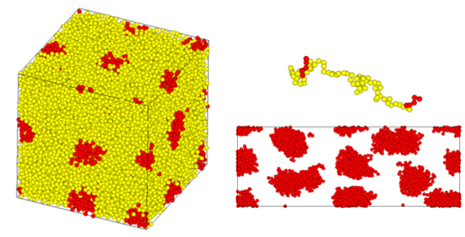
图3. 通过CGMD对三嵌段共聚物相分离结构进行单轴拉伸计算。（左图：初始结构，右图：变形下的结构（上图：单链，下图：领域结构））

4、耗散粒子动力学和平均场方法

耗散粒子动力学（DPD） 是CGMD的一种，但其使用允许粒子间相互作用穿越的软势使其适用于相分离和填充物分散结构的评估。动力学还包括水动力学效应。在平均场（MF）方法中，聚合物的每个组分表示为一个浓度（体积分数）场，用于评估相分离动力学甚至是平衡状态。它可以与每个组分的扩散和水动力学耦合。特别是，自洽场理论（SCFT）可用于考虑聚合物链的形状。在这些方法中，弗洛里-哈金斯χ参数用作组分（粒子）之间的相互作用。已经提出了使用FAMD和量子化学计算估计此参数的方法。

图4（左）显示了使用DPD计算的聚电解质和水的相分离结构，图4（右）显示了使用平均场方法计算的三组分聚合物系统的相分离（核/壳）结构。目标空间尺度为几百纳米。

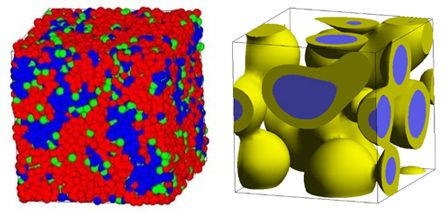
图4. 左图：DPD计算的聚电解质相分离结构，右图：平均场方法计算的三聚合物组分相分离结构

5、爬行动力学

通过将聚合物链以交缠点之间的分子量为单位进行粗粒化，可以计算基于聚合物链交缠结构的爬行动力学。方法包括滑动链模型和原始链网络（PCN）模型。近年来，滑动弹簧模型[7]能够将聚合物链交缠效应添加到DPD中。

图5是聚异戊二烯（分子量约48,800）的G'（存储模量）和G"（损耗模量）的评估。快照中的弯曲点对应于交缠点。

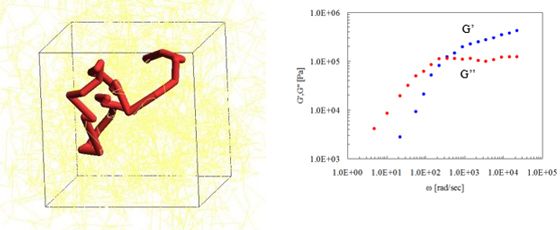
图5. 通过PCN评估粘弹性（左图：快照，右图：主曲线）

6、连续体模型

使用DPD和平均场方法获得的相分子结构，可以基于连续体模型进行有限元方法（FEM）计算，以评估平均弹性模量和热导率等物理性能。各组分的材料性能作为参数输入。图6（左）显示了在将变形施加到图4（右）中获得的相分离结构时，界面处的应变能分布；图6（右）显示了在聚合物中通过DPD获得的纳米填料分散结构进行热传导计算时的热通量分布。图6中的计算基于某种模拟得到的结构，但还有其他方法可以利用结构，如使用散射试验或CT的数据，或通过创建虚拟结构对物理性能和结构之间的关系进行数值实验。

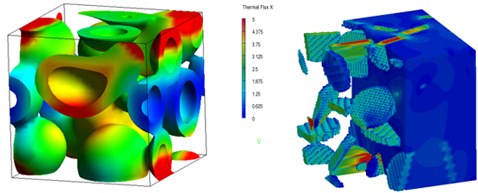
图6. 通过有限元方法评估力学性能

（左图：相分离结构中的应变能分布，右图：纳米填料分散结构中的热通量分布）

7、J-OCTA中包含的引擎（求解器）

对于量子化学和密度泛函理论，J-OCTA捆绑了SIESTA和ABINIT-MP，并提供了与Gaussian等的接口。对于全原子和粗粒化分子动力学，包含COGNAC、VSOP和GENESIS，并提供了与LAMMPS、GROMACS和HOOMD-blue的接口。耗散粒子动力学（DPD）类似于分子动力学，但未包含在GENESIS和GROMACS中。对于平均场方法，包含SUSHI。对于爬行动力学，包括COGNAC和VSOP的DPD功能与滑动弹簧模型、PASTA和NAPLES。对于连续体模型，适用于MUFFIN，并提供与其他商业CAE软件的接口。

更多行业解决方案，请联系我们：
全国热线 ：400 633 6258
官方网站 ：www.anscos.com
邮 箱 ：info@anscos.com

或扫描下方二维码填写表单，我们将尽快与您联系！