双螺杆压缩机是一种做回转运动的容积式气体压缩机械,随着螺杆转子的转动,阴阳转子间的齿间容积沿转子轴线从吸气端运动到排气端,且齿间容积由小到大再变小,发生周期性的变化,完成吸气、压缩和排气过程。
压缩机内温度的变化对压缩性能和效率有着至关重要的影响,为了准确地预测压缩机的热动力学特性,在CFD模拟中需要对金属部件与工作流体之间的传热进行适当的分析与评估。
本文基于Simerics-MP+软件,利用混合时间尺度耦合法求解不同介质间耦合传热的问题。该方法可以解决热传播的时间尺度差异问题。通过比较在有和没有考虑共轭传热情况下的模拟结果,评估流固共轭传热对双螺杆压缩机性能的影响。结果表明本文所使用的方法是有效、快速和友好的,可以很容易地应用于工业压缩机系统。
双螺杆压缩机具有2个结构特殊的转子,转子与机壳构成了一个复杂的空间,且阴阳转子间的间隙非常小,有时仅有几十微米,网格解析及运动定义困难。
通常,固体中热传播比气体中的慢得多,如果将固体内部的热传导与气体的热力学温度变化直接耦合,可能需要压缩机转子转很多圈数才能达到稳定的解,模拟花费的时间很长。
下面将以一个实例来说明流固传热时间尺度问题。
如图1所示,以实际双螺杆压缩机的固体转子作为本研究的最终测试案例,做一简单的热传导模拟来演示传热过程中的时间尺度差异。转子由不锈钢材料制成。转子初始温度设定为300K,转子叶片暴露在周围流体中,温度为400k。假设边界面上的最大传热系数为1000w /m2K,通过对转子内部瞬态热传导的快速模拟计算发现,经过一分钟的热传导后,固体转子的平均温度仅从300k提高到350k。
图2为热传导1分钟后的温度分布,其中转速约为8000转/分钟。因此,转子转动上万甚至十万圈后才能接近最终温度400k。仿真运行时间太长,不适合实际应用。瞬态模拟中还发现,在0.0075秒后,阳转子在8000 rpm转速下每旋转一圈,固体表面温度变化仅约为1 K。基于以上事实,构成了我们所提出的混合时间尺度耦合方法的基础。
以上简单的模拟结果证明,求解螺杆压缩机流体与固体之间的直接耦合传热是不经济的。在此基础上,提出了一种混合时间尺度耦合方法,该方法在获得稳定解所需的时间大大缩短的同时,仍能捕捉到较好的共轭传热效果。
本研究提出的耦合方法中,流体域和固体域作为独立的模型被计算,在流固交界面上交换热量作为每个模块的边界条件。
在流体模型中,将固体模型计算温度结果作为其边界条件。
在固体模型中,将流体模型平均每圈计算的热通量作为其边界条件。
迭代过程从流体模型的瞬态模拟开始,在流体/固体界面处设置恒定的初始温度;流体模型完成一个循环后,将界面热通量反馈到固体模型;固体模型进行稳态求解,收敛后将固体模拟得到的界面温度作为边界条件反馈回流体域;流体模型将进行下一个循环并更新的界面热流,直到界面热流和温度稳定收敛。
压缩机模型为一无油双螺杆压缩机,具有3/5齿布置和“N”转子廓形转子。阳转子的工作转速从6000到14000rpm不等,阳转子直径127.45 mm,阴转子直径为120.02 mm,两个转子之间的中心距为93.00 mm。转子的长径比为1.6,阳转子的包角为285.0°。仿真中采用了两个独立的模型:流体域模型和固体域模型。两个模型之间的耦合传热是通过迭代过程耦合在一起的。
在流体模型中,采用网格生成软件SCORG对双螺杆转子部分进行网格划分。SCORG为不同旋转角度的转子创建了一系列网格文件。通过Simerics - SCORG网格接口将转子网格文件读入求解器。利用Simerics二叉树非结构化网格对流体域的进出口进行网格划分。所有的流体体积通过不匹配的网格接口(MGI)连接在一起。流体域的网格总数约为145万个单元。流体域的网格如图5(a)所示。
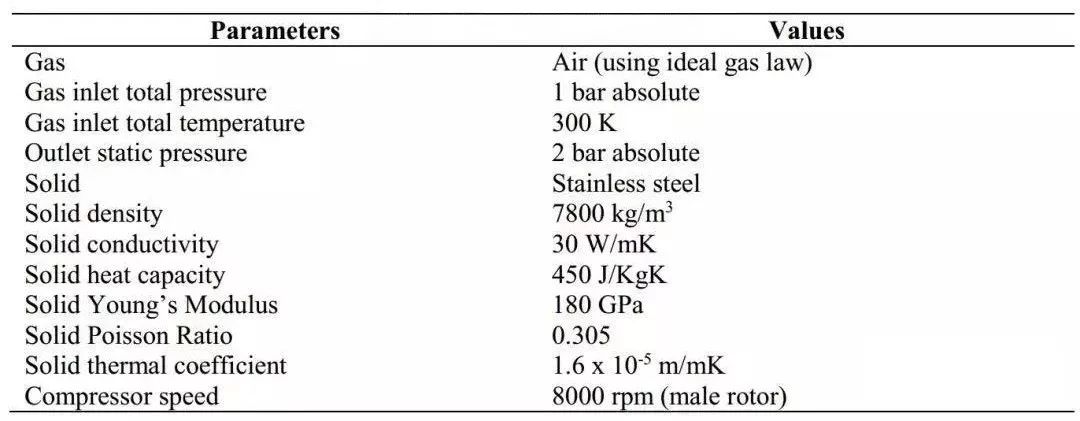
进气口设置为总压、总温边界条件,出口设置为静压边界条件。将流固界面设置为温度边界,具体温度数值由固体模型求解给出。模拟流体为空气,采用理想气体定律进行建模。外转子转速为8000转/分。为了验证流体与固体之间的耦合传热效果,还模拟了相同参数条件下,用绝热壁面求解流体-固体界面的传热算例并进行了比较。
固体模型包括三部分:机壳、阳转子、阴转子。全部使用二叉树划分网格,数量大约40万个单元。如图5 (b)所示,流固界面设置为固定热流边界,具体热流数值由流体模型求解给出。壳体外表面设置为热对流边界。固体模型求解稳态导热问题。与流体模型的仿真时间相比,固体模型每次运行的仿真时间可以忽略不计。
在仿真过程中,阳转子转动5圈左右时仿真结果开始呈现周期性变化。下图显示了流体和转子之间的瞬时和平均热通量。转子界面处流体与固体之间的最大瞬时热流约为400w,壳体外表面带走的平均热量约为100w。
最终计算的阳转子、阴转子、机壳平均固体域温度分别为345.3 K、349.0 K和329.6。图7 (a)为固体中心截面的温度分布,图7 (b)为转子表面温度。
图7 固体模型温度分布: (a)中心截面; (b)转子模型
彩色图例范围从300k到400k,洋红色代表高温,蓝色代表低温。从入口到出口,固体内部温度呈现由低到高的分层分布。作为对比,在流固界面建立了绝热壁面的流体模型,即不考虑流固共轭传热。在这种情况下,不同的曲轴角度下,界面温度不断的发生变化。
图8为在不考虑流固共轭传热情况下,五种不同曲轴转角下
(
分别为(a)24°;
(b)48°;(c)72°;(d)96°;(e)120°
)阳转子的温
度分布。
瞬时温度不再是由下至上分层渐变分布。相反,温度在每个腔体中有相似的值。而且,温度范围也明显更高。这意味着由于金属较大的热惯性,转子表面温度实际上比绝热壁面假设的温度更温和、更均匀、呈层状分布。
图9为考虑流固传热情况下,5个曲轴角度下(分别为(a)24°;(b)48°;(c)72°;(d)96°;(e)120°)转子的压力云图。
图中彩色图例范围从1bar到2.5bar,洋红色代表高压,蓝色代表低压。每个流体压缩腔中的压力与预期值相似。当压缩腔从入口移动到出口时,由于流体体积的逐渐减少,压力增加。与温度分布不同的是,转子表面的压力分布几乎是均匀的。这意味着共轭传热对压缩机性能的影响很小。
下表比较了有和没有考虑共轭传热情况下气体质量流量和转子功率的差异:
Gas mass flow rate
(kg/min)
可以看出,考虑和不考虑共轭传热相比,质量流量和转子功率的预测误差小于1%。与实验结果相比较,两种结果对流量的预测都高出约4-5%。这种误差可能是由间隙尺寸的不准确性引起的。功率预测与实验相差约1%。可以看出,对于该给定模型,流固耦合共轭传热对压缩机性能的影响很小,因此不考虑耦合传热的模拟结果是可以接受的。
基于固体温度模拟结果,利用Simerics-MP+ CFD软件包中的应变-应力求解器对固体热应力/膨胀进行了预测。上图描绘了由于径向热膨胀引起的转子固体位移。该彩色图例范围从0到50微米,洋红色代表高位移,蓝色代表低位移。径向最大位移约为50微米。需要注意的是,本文中的热膨胀是单向耦合预测。热膨胀的结果没有反馈到流体模型中。
基于Simerics-MP+软件,提出了一种求解共轭传热的混合时间尺度耦合方法,并成功地应用于双螺杆压缩机的建模计算;
将模拟结果与试验结果进行了对比,误差在5%以内,验证了该方法的可行性和准确性;
对有无共轭传热的模拟结果进行了对比,对于该给定模型,耦合传热对压缩机性能的影响很小;
基于温度结果的单相耦合,对固体热膨胀程度进行了预测。
文章来源:合工仿真

 当前暂无评论,小编等你评论哦!
当前暂无评论,小编等你评论哦!



















