超高速永磁同步电机(PMSM)具有转速高、径向力波阶数低等特点,但定子易共振引发较大噪声。以1台超高速PMSM为例,依据电机实际尺寸,建立了电机电磁场模型和定子结构的3D模态模型。采用有限元法对该电机的径向电磁力进行仿真,分析了引起电机振动的主要电磁力谐波次数,确认了电机电磁噪声的主要来源。最后,通过ANSYS声场的声压级云图研究了超高速PMSM的电磁噪声特性。
刘朋鹏, 王建辉, 韦福东
[上海电器科学研究所(集团)有限公司,上海 200063]
0 引 言
采用超高速永磁同步电机(PMSM)驱动的压缩机具有效率高、体积小、功率密度大等优点,在燃料电池中得到了广泛的应用。但超高速PMSM转速高,电机径向力波阶数低,轻量化的结构设计导致定子刚度较差易共振引发较大噪声,影响压缩机的使用体验,因此在超高速PMSM设计时不仅需要考虑电机的电磁性能指标,还需要关注电机的振动噪声特性[1-3]。
电机的振动噪声伴随电磁、结构、力学和声场等多个领域错综复杂的耦合关系,是一个复杂的多物理场问题。为了对电机进行准确的噪声分析,国内外许多学者已进行了研究[4-5]。张增杰[6]研究了小功率PMSM气隙磁场对电机产生的振动及辐射噪声的影响。张玉柱[7]基于MATLAB频谱分析的分析方法研究了永磁电机噪声声源。朱海峰[8]对异步电机电磁激振力进行了分析。郑江[9]研究了低速大转矩和高速恒功率车用PMSM电磁噪声特性。林巨广等[10]研究了8极48槽PMSM径向力波、噪声来源,并说明电机噪声受单壳体刚度、前后端盖影响。
本文以1台120 000 r/min的超高速PMSM为例,通过Maxwell计算定子内表面径向和切向电磁力时域密度分布,将该力密度作为激励源耦合到Mechanical中进行频域的谐响应分析,并将分析结果作为激励耦合到Harmonic Acoustic中,得到径向力波对电磁噪声的影响,根据电磁力波二维傅里叶变换及噪声声压级云图研究了超高速PMSM的电磁噪声特性。
1 电机径向力波分析
样机的基本参数如表1所示。根据表1尺寸参数建立的电机模型如图1所示。
表1 电机的基本参数

分析电机电磁力波的前提是准确计算出电机的气隙磁场,获得气隙磁场后,利用麦克斯韦应力张量法就可推导出电机电磁力波。其计算式为
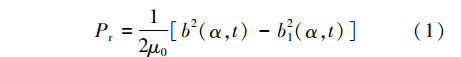
式中:Pr为电机径向力波和切向力波;μ0为真空磁导率,μ0=4π×10-7 H/m;b(α,t)、b1(α,t)分别为气隙磁通密度的径向和切向分量。
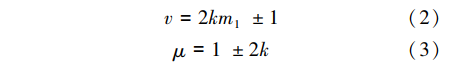
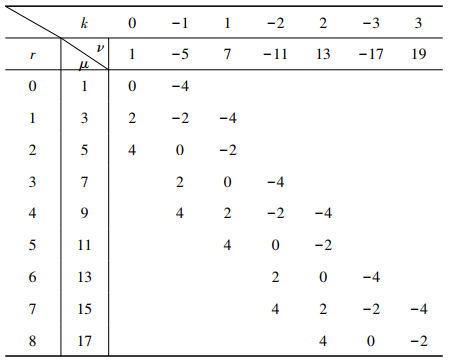
式中:v、μ为定子、转子的空间谐波次数;k=0,1,2,3,…;m1为相数。
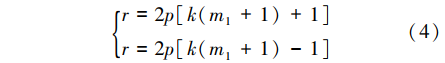
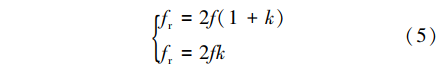
式中:r为力波次数;p为电机极对数;f为电源频率;fr为振动频率。
当仅考虑定子铁心周向振动模态时,定子铁心的形变量Δd与电磁力波次数的4次方成反比,即:
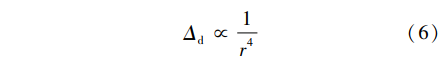
因此,对于小型电机,最重要的周向模态振型是低阶阶数(r=0,1,2,3,4,5),而当力波阶次较大时,其对应的阶次模态固有频率大,不会共振产生噪声。由以上分析可以得到电机的主要电磁激振力,表2列出了阶次小于4阶的电磁激振力波。
表2 电机的电磁激振力谐波次数
由Maxwell仿真可得电机径向、切向磁密b(α,t)、b1(α,t)如图2所示。
根据麦克斯韦应力张量法可得电机气隙径向力波,为时间和空间的函数,对某一时刻随空间位置变化的电磁力进行傅里叶分解,可得电磁力的空间阶数r;对气隙某一点随时间变化的电磁力进行傅里叶分解,可得电磁力的时间频率f。电机电磁噪声分析时,需确定电磁力波空间阶数和时间频率各自的对应关系,一次FFT分析不能完全反应径向力波中的谐波分量幅值,需要对电磁力进行时间和空间FFT分解,2次FFT分解结果如图3所示。
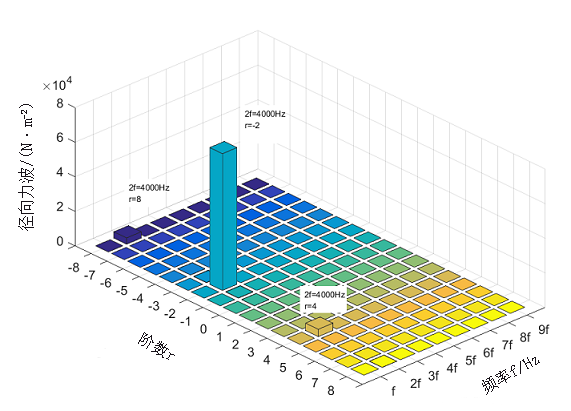
由于0力波不会产生振动噪声,以此将0力波分量删除,由图3可知径向力波幅值最大的分量为2阶2f谐波,其次为4阶2f与8阶2f谐波分量,但幅值均较小,原因是该超高速电机气隙磁密谐波少,径向力波基本只有2f基本力谐波。
对于电机定子而言,除了频率接近或相同之外,还需要考虑电磁力波的波形也需要与定子某一阶模态振型相近或相同。即当径向电磁力波某一阶次与定子空间模态振型相同,且电磁力波的频率与定子这一阶模态频率接近或相等时,定子会发生共振,故电磁力波需要从振型和频率上与电机定子的模态阶次避开,以减少电机定子系统产生的电磁噪声。因此,研究高速电机定子模态具有重要的意义。
图4为笛卡尔坐标系下电机定子0阶、2阶、3阶、4阶、5阶、6阶模态,频率分别为20 948、6 006.6、13 648、18 135、19 505、19 804 Hz,结果表明4阶以上模态频率较高,不易使定子振动,2阶模态频率较低,且径向力波存在多个频率的分量,当径向力波频率接近模态频率时可能共振产生较大噪声,另外需要关注0阶呼吸模态,频率较高但阶数低,较小的力波共振也会引起较大电机噪声。
将定子齿部电磁力施加到模态分析相同的模型上,进行有限元谐响应分析,在谐响应中,振动幅值与力波幅值成正比,低次谐波的幅值较大容易引起振动。但是当特定阶激振力波的频率与对应模态的固有频率相接近时,即使力波幅值很小也会引起较大的振动响应。
因为该电机Z轴方向电机振动幅值较小,所以仅给出了电机定子表面X轴和Y轴方向最大振动位移幅值,如图5所示。
由图4、图5(a)可知电机在6 000、13 600、18 200、19 800 Hz会有振动幅值尖峰,分别对应2阶、3阶、4阶及频率相近的5阶、6阶模态,其中2阶模态振动幅值远高于其他模态阶数;从图5(b)标出的电机2f、4f、6f、8f力波频率点可知,在二倍基波频率点振动幅值最大,但超高速电机定子较小刚度好,固有频率高于二倍基波频率,不会引起较大的噪声。
建立半径1 m包裹电机定子空气球噪声仿真模型,对该谐响应状态下电机噪声进行仿真,120 000 r/min时电机定子表面二倍基波频率声压级与电机整体声压级云图如图6所示。由图6(a)可知,尽管电机二倍基波频率点振动幅值最大,但不会与电机共振,噪声很小;
由图6(b)可知,由于电机气隙磁密正弦度较好,电机整体最大噪声为53.3 dB(A),电磁噪声较小,符合电机设计要求。
针对超高速PMSM转速高、电机径向力波阶数低、定子易共振引发较大噪声等特点,本文以1台超高速PMSM为例,依据电机实际尺寸,建立了电机电磁场模型和定子结构的3D模态模型。通过电机结构和电磁力波分析了电机电磁噪声,并得到以下结论:
(1) 二倍基波频率点振动幅值最大,但超高速电机定子较小刚度好,固有频率高于二倍基波频率,不需要过多关注此力波振动。
(2) 电机额定转速120 000 r/min运行时,电机力波阶数、频率与模态阶数、频率均不重合,不会共振引起较大的噪声。
本文为行业设计人员分析电机噪声提供了方法,提高了超高速电机噪声分析的准确性与可靠性,目前已完成样机试制,后续将对电机噪声进行进一步的测试验证。
 2023年6月16日 11:39
2023年6月16日 11:39





















