电磁振动噪声水平是衡量电动汽车舒适性的综合指标。径向电磁力是电磁振动噪声的主要激振源。对电动汽车驱动用永磁同步电机(PMSM)的径向电磁力进行分析,对径向电磁力时空分离得到的三维频谱图提取出对电磁噪声影响较大的时空阶次及力密度,再运用有限元法对转子不同方式分段斜极的PMSM进行振动噪声仿真,通过结果对比找到最优的转子分段斜极方式。
转子不同方式分段斜极对永磁同步电机噪声的影响
范庆锋1,2,王光晨1,2
(1.中车株洲电机有限公司,湖南 株洲412001;2.湖南省新能源汽车电机工程技术研究中心,湖南 株洲412001)
随着新能源汽车领域的发展,驱动电机各方面的性能不断提升,对电磁噪声提出了更高的要求。因为电磁噪声主要来源于电机驱动系统,所以驱动用永磁同步电机(PMSM)的噪声水平直接影响电动汽车的舒适性[1-3]。
PMSM电磁力可分为切向电磁力和径向电磁力2种,前者主要用于输出电磁转矩,但会引起转矩脉动,使定子齿部弯曲变形;后者使电机的定子铁心产生周期性形变而引起振动噪声,是引起电机振动噪声的主要原因[4-5]。
电机的振动噪声涉及电磁、机械、力学、声学等多个领域,研究方法主要有解析法、有限元法和试验法[6]。文献[7]通过对8极48槽PMSM进行了不同斜极分段数的径向电磁力仿真,分析了不同斜极分段数下电磁力波主要阶次的变化规律和对振动噪声的影响,但并没有研究不同斜极方式对电机振动噪声的影响;文献[8]研究了转子分段斜极与径向电磁力的之间关系,但并没有进一步研究对电磁噪声的影响;文献[9]提出了转子通过分段斜极以削弱齿谐波,降低0阶电磁力的改进方案,降低了电机的电磁噪声,但没有分析径向电磁力对电磁振动的影响。研究转子不同方式分段斜极对电磁振动噪声的影响对电磁振动噪声的研究和抑制具有一定的意义,但目前国内相关研究较少。
本文
以1台额定功率100 kW的纯电动客车驱动用PMSM为研究对象,利用有限元方法对电磁振动噪声进行仿真计算,通过对比分析转子不同方式分段斜极的谐响应和声场结果,得到最优的转子斜极方式。
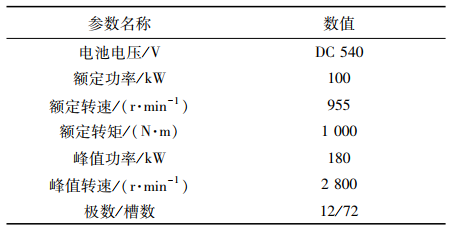
本文用于振动噪声研究的PMSM转子拓扑如图1所示。PMSM参数如表1所示。
表1 PMSM参数
定子铁心受到的径向电磁力远远大于切向电磁力,且在电机运行的过程中随着时空交变,是电磁振动噪声的主要激振源,因此本文只考虑径向电磁力。由于磁导率的影响,
切向气隙磁密远
远小于径向气隙磁密,前者
可忽略不计
,则径向电磁力密度可以近似表示为
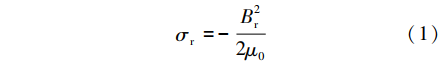
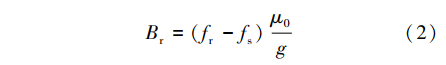
式中:fr为转子永磁磁动势;fs为定子电枢反应磁动势;g为气隙长度。
对定子电枢反应磁动势和转子永磁磁动势进行傅里叶分解,可得:
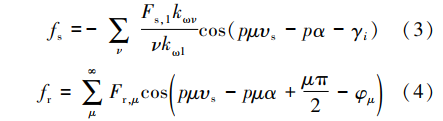
式中:ν为电枢反应磁场谐波次数;Fs,1为定子电流产生的基波磁势幅值;kων、kω1为绕组系数;p为极对数;υs为定子参考位置;α为旋转角;γi为电流角;μ为转子永磁磁场谐波次数;Fr,μ为永磁体产生的谐波磁势幅值;φμ为转子磁动势初相角。
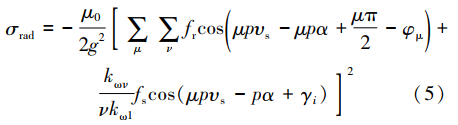
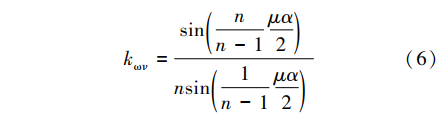
由于α为转子分段斜极的机械角度,则各转子铁心段之间错开的角度αt与分段数n有关,可以表示为
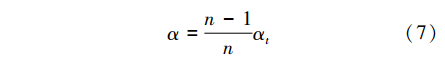
只考虑定转子之间的耦合作用,径向电磁力密度可以表示为
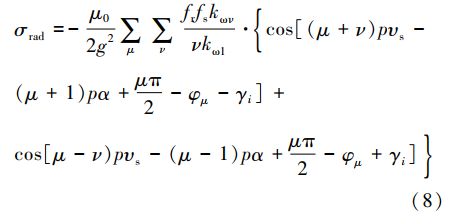
当μ=ν或μ=-ν时会产生空间0阶次的电磁力,该阶次的电磁力对振动噪声的影响最大,
因此主要关注空间0阶次下电磁力密度大的电磁力[10]
。
在转子分段不斜极的情况下,对本文研究的12极72槽PMSM空载和额定负载工况下的电磁力进行时空分离得到三维频谱图,从中找出引起振动噪声主要电磁力波的时空阶次及电磁力密度,如图2所示。
电磁振动噪声影响较大的电磁力波时空阶次和力密度,如表2所示。
表2 径向电磁力波阶次及力密度
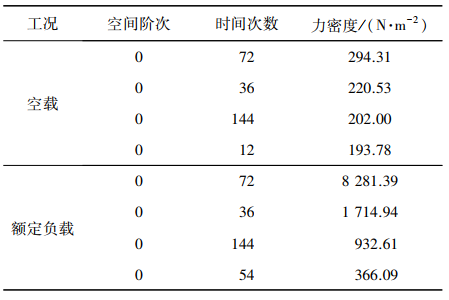
从表2可以看出,
空载和额定负载工况下,空间阶次为0、时间次数为72的电磁力密度均是最大的,对电磁振动噪声的影响也是最大的,主要由11次和13次谐波引起
;其次空间阶次为0、时间次数为36的电磁力,对振动噪声的影响比较大,主要由5次和7次谐波引起[11-13]。
由于72阶电磁力密度最大,重点分析不同斜极方式下72阶电磁力对振动噪声的影响。
为了验证不同分段斜极方式对电机振动噪声的影响,应用ANSYS有限元法对PMSM振动噪声进行仿真分析。该纯电动客车驱动用PMSM采用12极72槽的配合方式,转子分段斜极一个定子齿距5°,分别建立不同方式的转子分段斜极的电磁模型进行振动噪声仿真。
转子分段斜极不仅能够削弱谐波,优化齿槽转矩和转矩脉动,还能有效降低径向电磁力造成的振动噪声[14]。
转子斜极方式和分段数的选取均对电机的振动噪声有影响。本文将转子铁心分为6段,对转子进行
分段不斜极、Z型斜极、单边斜极和双边斜极
的处理,分别对4种转子进行振动噪声的仿真分析,如图3所示。
在上述分段斜极的基础上,以第一段为参考,汇总各段错开的机械角度,如表3所示。
表3 转子不同斜极方式下各段错开角度 (°)

建立PMSM定子的三维模型,用于谐响应分析和声场仿真计算;选取驱动电机最大外特性曲线上的工作点按转速为增量添加到各电磁仿真模型,将随转速变化的电磁力分别添加到各段定子铁心模型的对应齿上,再添加约束条件、求解设置,得到电机的谐响应分析结果[15]。
在谐响应计算结果中提取出随转速逐渐变化的36阶和72阶等效辐射功率,如图4所示。
汇总不同斜极方式中36阶和72阶等效辐射功率的最大值,如表4所示。
表4 不同斜极方式的最大等效辐射功率 (dB)
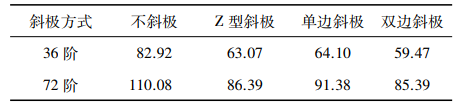
(1) 随着转速的增加,每个阶次的等效辐射功率均呈上升状态,斜极方式不同,但均表现为72阶最明显,其次是36阶,这与电磁力时空分离的结果相吻合,主要与电机的12极72槽配合有关。
(2) 对于不同斜极方式产生的等效辐射功率而言,转子分段不斜极的效果最差,辐射功率最大值为110.08 dB,其次是单边斜极、Z-Z型斜极,双边斜极的等效辐射功率最低,为85.39 dB,效果最优。
在上述谐响应计算结果的基础上进行电机多转速工况的噪声仿真。建立电机声场的仿真模型,在电机外表面构建1 000 mm的空气包络,并对其进行网格剖分、导入载荷和声域求解设置,仿真计算得到电机的声场结果。
从不同斜极方式的声场计算结果中提取随转速变化的36阶和72阶声功率曲线,如图5所示。
不同斜极方式下36阶和72阶声功率的最大值如表5所示。
表5 不同斜极方式的最大声功率 (dB)
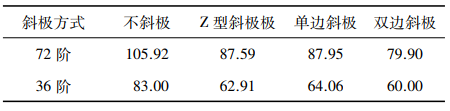
由以上分析可以看出,对于本文所研究的驱动用PMSM而言,转子分段不斜极的效果最差,
转子双边斜极的效果最好
,二者的最大声功率相差26 dB,声场计算结果如图6所示。
(1) 不同斜极方式的36阶和72阶声场计算结果与谐响应分析的结果基本一致,均随着转速的增加呈上升趋势,且72阶表现的最明显。
(2) 转子分段不斜极时的声功率最大,为105.92 dB;其次是单边斜极、Z型斜极;双边斜极的声功率最低,降噪效果最优,最大值79.90 dB。
本文以1台额定功率100 kW的纯电动客车驱动用PMSM为例进行转子不同方式分段斜极的振动噪声仿真,通过对比分析得到以下结论:
(1) 电机产生的振动噪声主要受径向电磁力的影响,该径向电磁力主要与极槽配合有关。本文采用12极72槽的配合方式,72阶电磁力对振动噪声的影响最大,其次是36阶电磁力。
(2) 在转子分段数相同的情况下,转子斜极方式不同,对振动噪声的削弱也不一样,对于本文所研究的电机而言,双边斜极产生的振动噪声最低,效果最好。
文章来源:电机与控制应用
 2023年6月19日 15:50
2023年6月19日 15:50





















