关键词:Mullins效应 永久变形 应变循环
材料损伤 能量耗散 材料校准
1. 问题描述及材料校准
实心圆盘的外径3in,内径1.75in,厚度0.7in。使用对称模型生成功能建立三维模型,单元类型为一阶缩减积分四面体单元(C3D8R),同时使用增强沙漏控制选项。材料属性包括Mullins效应、永久变形(用金属塑性材料模型模拟)、超弹性(Yeoh材料模型)。Mullins效应是填充橡胶材料发生变形时产生的应力软化现象。本例包括以下三方面的分析:
已知的数据包括一组单向试验数据、一组应力-塑性应变试验数据、0.099/0.26/0.51应变水平的加载/卸载循环变形试验数据。输入这些数据,对单位单元的变形进行分析,将得到的响应曲线与试验数据进行比较和评估,获得相应的材料参数。如下图所示,单位单元经历0.099/0.26/0.51三个应变水平的变形循环。
定义
Yeoh
超弹性、Mullins效应、塑性变形属性
的关键字如下:
** 定义材料模型*MATERIAL,NAME=材料名称*HYPERELASTIC,YEOHC10,C20,C30,D1** *HYPERELASTIC,YEOH,TEST DATA** *UNIAXIAL TEST DATA** 应力1,应变1** 应力2,应变2** ......*MULLINS EFFECT,TEST DATA INPUT*INCLUDE,INPUT=试验数据文件名.inp*plastic应力1,塑性应变1应力2,塑性应变2......*DENSITY材料密度** Mullins应变循环试验数据格式(单个应变循环)*UNIAXIAL TEST DATA应力1,应变1应力2,应变2......** 输出单元能量损耗*ELEMENT OUTPUT,ELSET=单元集DMENER,** 定义节点自由度耦合方程*EQUATION方程中的项数节点编号/集合1,自由度1,系数1,节点编号/集合2,自由度2,系数2,......
静态分析中,圆盘与刚性平面接触,通过刚性面的位移来控制结构的变形。第一个循环最大位移为0.15in,第二个循环最大位移为0.22in。作为对比,分别使用Abaqus/Standard和Abaqus/
Explicit两种分析方法。
滚动分析中,刚性面先位移0.15in,然后在圆盘上施加2.5rad/s的角速度。作为对比,将分别使用Abaqus/Standard静态、Abaqus/Standard稳态传输和Abaqus/Explicit三种分析方法,均不考虑摩擦和惯性效应。滚动分析相比于静态分析的网格应适当细化。在显式分析中,参数要做适当调整以增大时间步长,位移幅值选择平滑选项,并监控总动能以保证问题的准静态属性。在稳态传输分析之前,需要附加一个角速度0.25rad/s且Mullins效应渐变的稳态分析步,以克服收敛困难。
定义
运动耦合
、平滑幅值、渐进损伤稳态分析
的关键字如下:
** 定义运动耦合*COUPLING,CONSTRAINT=耦合名称,REFNODE=参考节点编号,SURFACE=要耦合的面*KINEMATIC起始自由度,结束自由度** 定义显式分析的平滑幅值*amplitude, definition=smooth step, name = 加载幅值名称 0.0, 0.0, 1.0, 1.0*amplitude, definition=smooth step, name = 卸载幅值名称 0.0, 1.0, 1.0, 0.0** 定义渐进损伤稳态分析*STEADY STATE TRANSPORT,MULLINS=RAMP初始子步长,步长,
下图是该单元的应力-应变曲线与试验数据的对比,其中分别是超弹性试验数据、0.099/0.26/0.51应力水平的变形循环数据、单元应力-应变曲线。在.dat文件中得到Yeoh超弹性模型的参数C
10
=191.32,C
20
=4.94,C
30
=0.53,并使用微小的可压缩参数D
1
=5E-6(显式分析中为5E-5)。在后续计算中,超弹性通过输入以上参数实现,但Mullins效应属性和永久变形属性则直接通过输入试验数据实现。因为在计算过程中,Abaqus会自动进行材料数据转换。可以看出在指定的应力水平下,分析得到的卸载/加载循环是单一曲线,这与试验数据不同。这是因为试验过程中材料是渐进损伤的。
下图是Abaqus/Standard和Abaqus/Explicit分析的圆盘静态反力-位移和损伤-时间历程数
据。图中包括两个变形周期。
在第一个周期中,由于Mullins效应损伤,卸载响应比加载响应更软。在第二个周期中,未
超过0.15 in位移的响应与第一个周期的卸载过程相同。超过这一点,响应是第一个周期加载段的外延。
在第一个周期的加载过程中,随着变形引起损伤的增加,能量耗散也增加。在第一个周期的卸载过程中和第二个周期的加载过程中,位移达到0.15 in之前,损伤都不会增加,能量耗散也不会增加。当位移超过0.15 in之后,损伤进一步增加,能量耗散也进一步增加。在最后的卸载过程中,能量损耗保持不变。
虽然Abaqus/Standard和Abaqus/Explicit仿真的位移-时间历程不同,但总位移是相同的。结果表明,两种分析的能量损耗-时间历程在斜率上存在一定差异,但每个阶段结束时的总能量耗散是相同的。
以下两
图是滚动分析中的反力和反力矩响应曲线。fefp表示考虑永久变形的拉格朗日法分析、lagr表示不考虑永久变形的拉格朗日法分析、sst表示不考虑永久变形的稳态传输分析。
反力结果表明,在加载过程中反力增大。在圆盘第一圈旋转时减小。反力的减少是材料损伤的结果。在圆盘第二圈旋转时,反力保持不变,损伤保持不变。包含与不含永久变形相比结构更软,并且当圆盘在刚性平面上滚动时,压痕区域中存在永久变形。在附加的稳态传输分析步中,反力逐渐过渡,逐渐增加Mullins效应。在正常的稳态传输分析步中,反力保持在前一分析步结束时的值,这说明了Mullins效应损伤与旋转角速度无关。
反力矩结果表明,如果无Mullins效应,则接触力关于一个与刚性平面垂直且过轴的平面对称,旋转圆盘应无反力矩。然而,由于Mullins效应损伤,接触力是不对称的。第一圈旋转时的反力矩不是零,第二圈旋转时反力矩减小到零(损伤不再增加)。稳态传输分析结果不包括第一次旋转的瞬态解,反力矩始终为零。
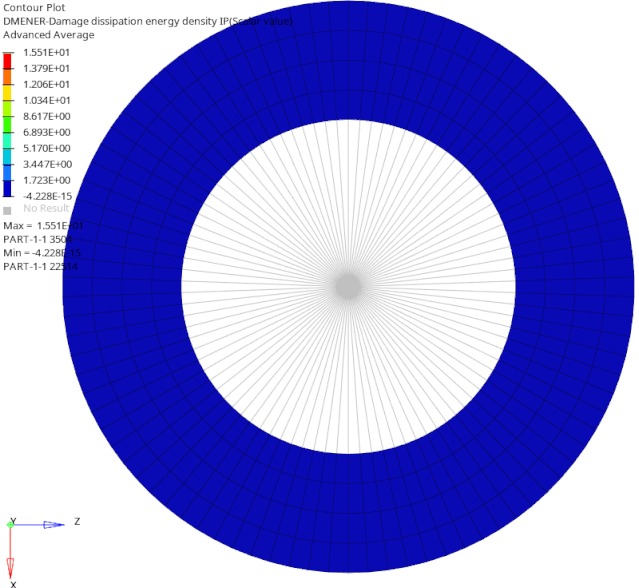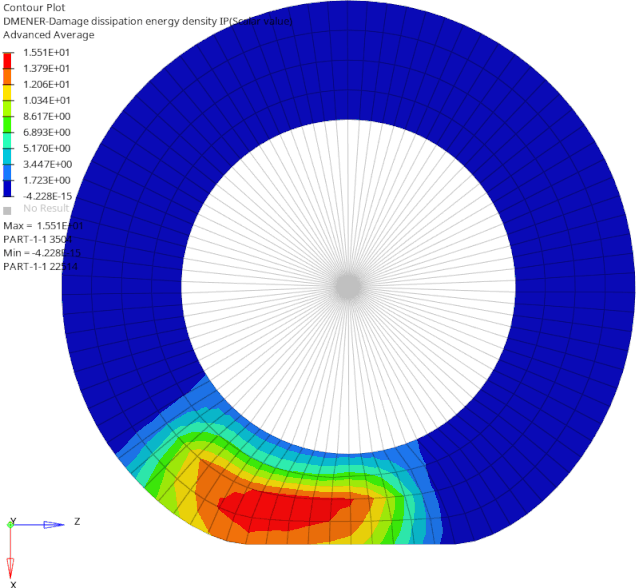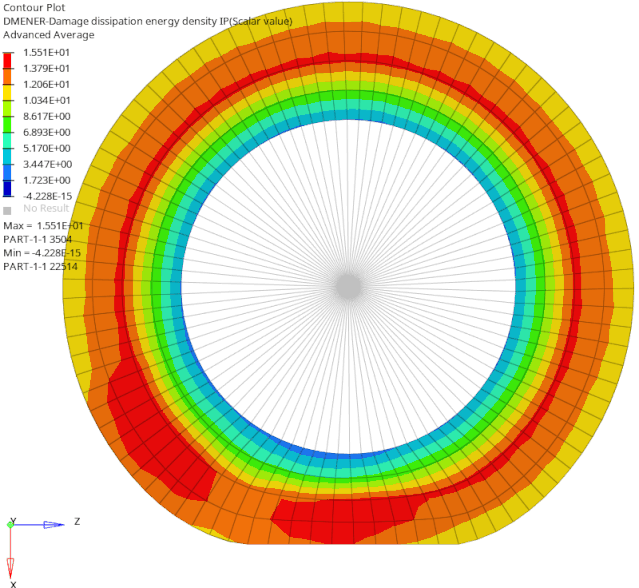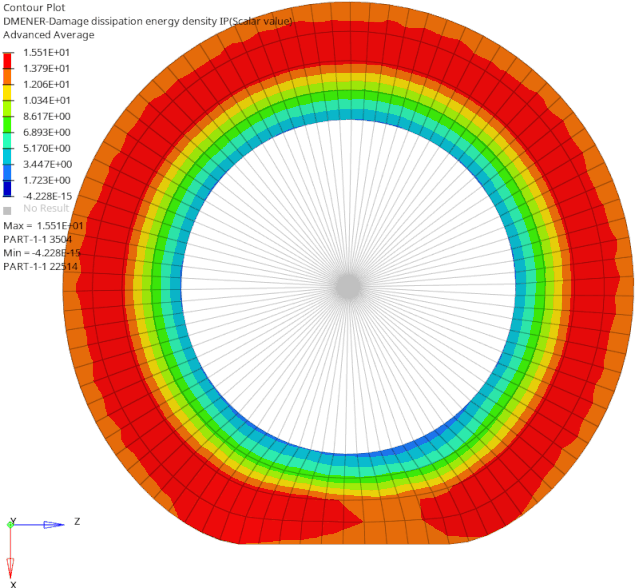
下图是旋转四分之三圈时的能量耗散和永久应变云图。结果表明,已通过接触区域的材料有损伤和永久变形,尚未通过接触区域的材料中无损伤或永久变形。
以上讨论,清楚地说明了Mullins效应造成的材料损伤过程及其影响。
文章来源: CAE仿真实例






















