很多材料都具有各向异性的特性,并且在很多情况下,各向异性与材料的形状相关。COMSOL Multiphysics® 软件提供了多种定义曲线坐标系的方法(曲线坐标系可作为局部坐标系来定义材料的各向异性)。这篇文章,我们将讨论每种曲线坐标系定义方法的概念以及如何进行选用。
各向异性特性
各向异性特性广泛存在于各个领域,例如,具有地震各向异性的岩层、液晶显示器中使用的液晶、航空工业中使用的轻质但仍能承受高负荷的材料,或者最接近生物软组织性能的医疗替代品,等等。
曲线坐标系的基础知识
让我们了解一下这个案例,考虑一种碳纤维增强聚合物,其中嵌入环氧树脂基体中的编织纤维沿纤维轴向具有较高的热导率,在横截面上具有较低的热导率。如果想要使用熟悉的笛卡尔坐标系来表示纤维的各向异性几乎是不可能的。但是,如果有一个跟随纤维走向的坐标系,就可以直接设置各向异性特性。
环氧树脂基体中的编织纤维。
如何确定这样的坐标系呢?在物理学上,有许多效应会产生跟随几何形状的矢量场,例如,顺着纤维的流动,或者从纤维一端到另一端的热传导,甚至是产生磁场的一束载流导线。这些正是 COMSOL® 软件中用来计算曲线系统的方法,所有这些方法都可以用来计算构成第一基矢 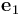 的矢量场
的矢量场 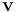 。由于大多数应用需要归一化的矢量场,COMSOL Multiphysics 会自动除以
。由于大多数应用需要归一化的矢量场,COMSOL Multiphysics 会自动除以 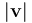 进行归一化处理。第二个矢量场可以手动指定,笛卡尔坐标通常是一个不错的选择。以此为起点,我们重建第二基矢
进行归一化处理。第二个矢量场可以手动指定,笛卡尔坐标通常是一个不错的选择。以此为起点,我们重建第二基矢 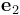 ,确保它与
,确保它与 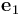 垂直,并被归一化处理。最后,这两个矢量的叉积得到第三基矢
垂直,并被归一化处理。最后,这两个矢量的叉积得到第三基矢 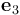 。
。
在软件内部,使用直角坐标系 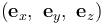 进行计算,并将所有涉及不同坐标系的量转换到
进行计算,并将所有涉及不同坐标系的量转换到 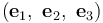 坐标系。任意坐标系中,由矢量
坐标系。任意坐标系中,由矢量 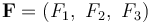 给出的方向总是可以转换为笛卡尔坐标,如下所示:
给出的方向总是可以转换为笛卡尔坐标,如下所示:
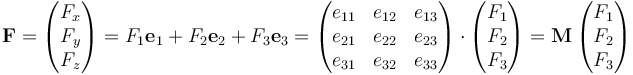
式中,
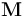 是变换矩阵。对于逆变换,只需使用逆
是变换矩阵。对于逆变换,只需使用逆
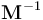 ,如果
,如果
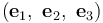 是正交的,那么
是正交的,那么
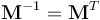 。
接下来,我们来介绍 COMSOL Multiphysics 中可用于计算曲线坐标系的不同方法,包括:
。
接下来,我们来介绍 COMSOL Multiphysics 中可用于计算曲线坐标系的不同方法,包括:
扩散方法
扩散方法求解拉普拉斯方程:
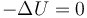 。解
。解
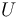 是一个标量势,它的梯度构成了第一基矢。因为只求解一个标量势,所以这个方法的计算成本很低。矢量场的方向由入口和出口的边界条件指定。如果几何结构是一个闭环,我们可以在内部边界上设置突变边界条件来指定方向。
扩散法相当于在入口和出口边界温度不变的情况下求解稳态热传导方程。然后,温度梯度形成第一基矢,如下图所示。
是一个标量势,它的梯度构成了第一基矢。因为只求解一个标量势,所以这个方法的计算成本很低。矢量场的方向由入口和出口的边界条件指定。如果几何结构是一个闭环,我们可以在内部边界上设置突变边界条件来指定方向。
扩散法相当于在入口和出口边界温度不变的情况下求解稳态热传导方程。然后,温度梯度形成第一基矢,如下图所示。
 曲线坐标系(箭头)、温度梯度(流线)和温度(表面)。
曲线坐标系(箭头)、温度梯度(流线)和温度(表面)。
自适应方法
自适应方法与扩散方法类似,也是基于拉普拉斯方程求解的。此外,该方法所得到的矢量场与几何结构相适应,能使流线密度在几何横截面上保持恒定。在使用
AC/DC 模块
(COMSOL Multiphysics 的一个附加产品)模拟 3D 磁应用时,这个公式被用于建立多匝线圈(线束)模型。对于多匝线圈,因为假设每根导线携带的电流相同,且导线的间距均匀,所以电流密度在横截面上应该是大致恒定的。
流动方法
流动方法求解不可压缩斯托克斯方程的一个矢量场和一个标量,因此这种方法在计算上是最耗费资源的。其边界条件与扩散方法相同,一个物理上的类比是不可压缩的蠕动流,在入口处有恒定的法线速度,出口处有固定的压力。产生的速度场得到第一基矢。
 曲线坐标系(箭头),速度场(流线),和压力(表面)。
曲线坐标系(箭头),速度场(流线),和压力(表面)。
弹性方法
其中,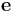 是矢量场,
是矢量场,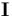 是单位矩阵,
是单位矩阵,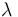 是特征值。
是特征值。
与流动方法相比,这种方法的计算成本略低,因为只求解一个矢量场。这种性能上的差异在 2D 模型中更为明显。其入口和出口的边界条件相同,即,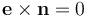 。在使用自适应方法之前,这种方法被用于模拟多匝线圈,因为它可以产生最佳的截面恒定流线密度。
。在使用自适应方法之前,这种方法被用于模拟多匝线圈,因为它可以产生最佳的截面恒定流线密度。
 曲线坐标系(箭头),线圈方向(灰色流线)和磁通密度(红色流线)。
曲线坐标系(箭头),线圈方向(灰色流线)和磁通密度(红色流线)。
除了这些预定义的方法外,COMSOL® 软件还像往常一样提供用户定义的输入。你可能会遇到想要手动实现曲线坐标的其他情况,比如用于模拟
动脉壁胶原软组织的各向异性超弹性材料
。
应该如何选择?
乍一看,所有方法产生的坐标系结果相同。然而,有些几何结构需要特别注意,当将坐标系应用于不同物理场时,选择不同的方法会产生明显不同的结果。对于有以下至少一项特征的几何结构,需要特别注意。
曲率
仔细观察各种方法的流线。请注意,这些流线按照定义了第一基矢的矢量场,从等距离的点开始,但遵循不同的路径,如下图所示。
 扩散法:流线遵循”最短”路径。
扩散法:流线遵循”最短”路径。
 自适应方法:均匀分布的流线。
自适应方法:均匀分布的流线。
 弹性方法:流线倾向于在凸形弯道处积聚。
弹性方法:流线倾向于在凸形弯道处积聚。
 流动方法:流线倾向于在凸形弯道处积聚。
流动方法:流线倾向于在凸形弯道处积聚。
如果弯道非常尖,每种方法的差异就更加明显,而自适应方法也可能会形成非均匀的流线密度。
变化的截面
在这种情况下,使用弹性方法可能会失败,得到的特征值与特征向量并不能产生所需的坐标系,而且我们可能不得不手动搜索正确的特征值。由下图可以看到,在几何结构的上部,流线也没有完全遵循形状。扩散法和自适应法也有类似的行为,但没有那么明显。在这个情况下,流动方法产生了最好的结果,但计算量也最大。
沿着几何结构中心平面的流线。
传热应用
回到我们的纤维模型,在纤维方向上的各向异性热导率为
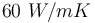 ,而垂直于此方向的热导率为
,而垂直于此方向的热导率为
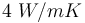 。如果这些方向与坐标系的轴线重合,则二阶张量热导率有 0 个对角线单元。
为了能够使用这种对角线形式,必须在求解传热之前计算纤维的曲线坐标系。由于几何结构没有急剧的弯曲或变化的横截面,因此使用扩散方法可以快速得到曲线坐标系的解。
之后,可以在纤维中的传热节点中参考这个坐标系。热导率的各向异性可以在材料节点中定义,使用语法
。如果这些方向与坐标系的轴线重合,则二阶张量热导率有 0 个对角线单元。
为了能够使用这种对角线形式,必须在求解传热之前计算纤维的曲线坐标系。由于几何结构没有急剧的弯曲或变化的横截面,因此使用扩散方法可以快速得到曲线坐标系的解。
之后,可以在纤维中的传热节点中参考这个坐标系。热导率的各向异性可以在材料节点中定义,使用语法
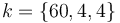 。或者,可以在相关的传热节点中选择用户定义的输入。
。或者,可以在相关的传热节点中选择用户定义的输入。
相关传热节点中各向异性的定义。
在该模型中,一个高斯脉冲形式的边界热源被施加到几何结构的中心,温度沿着纤维扩散。
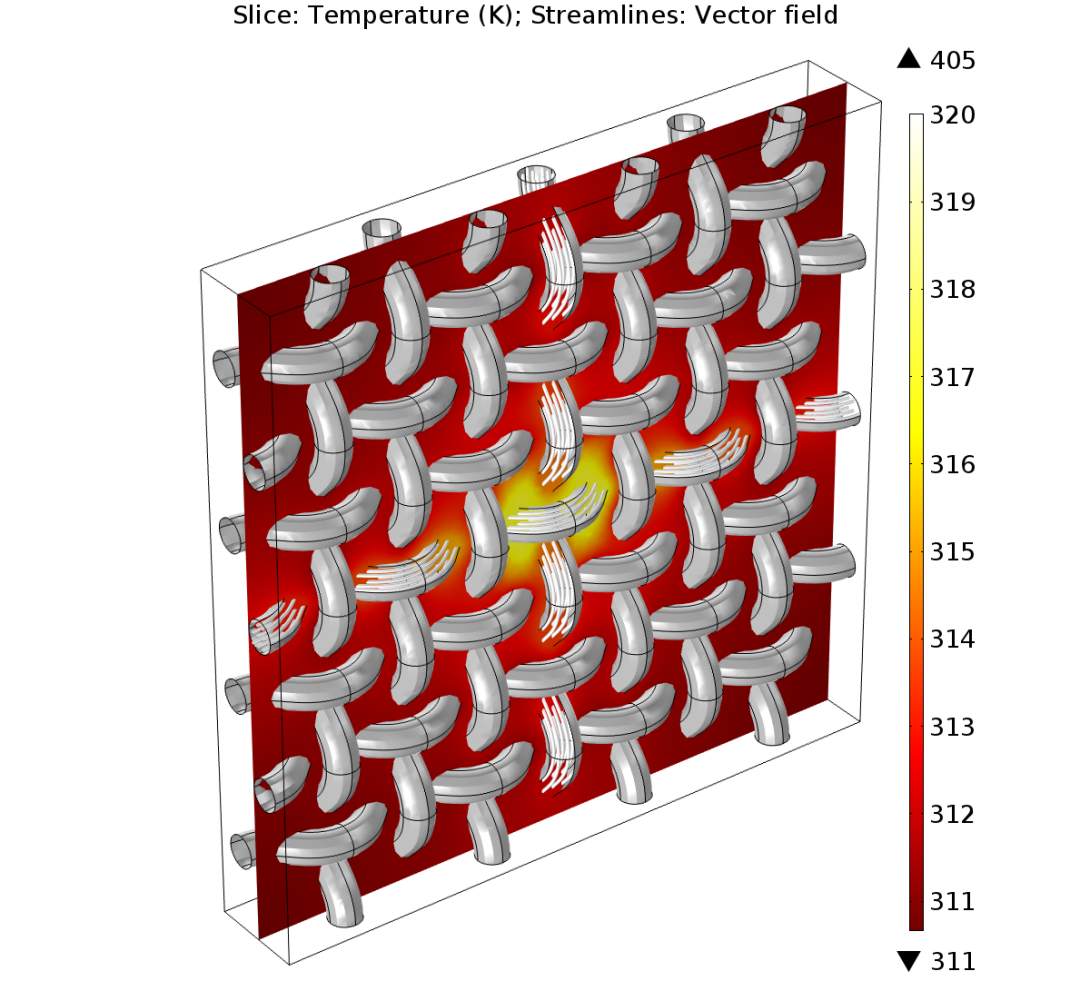 流线表示用曲线坐标接口得到的矢量场。
流线表示用曲线坐标接口得到的矢量场。
如果想直观地观察结果,例如,查看热导率的 xx 分量(
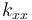 ),则需要在直角坐标中绘制 xx 分量
),则需要在直角坐标中绘制 xx 分量
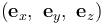 。根据上面描述的变换,纤维的热导率张量,
。根据上面描述的变换,纤维的热导率张量,
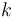 ,是非对角线形式的。用于定义
,是非对角线形式的。用于定义
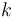 的局部基矢量系统,
的局部基矢量系统,
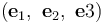 ,现在经过空间变化变为
,现在经过空间变化变为
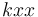 。在这个模型中,您还可以在切面图中绘制例如热导率矢量等分量,可以在相应的设置窗口的表达式 菜单中选择它们,或者简单地输入 ht.kxx(其中 ht 是用于该模型的固体传热接口的标签)。
。在这个模型中,您还可以在切面图中绘制例如热导率矢量等分量,可以在相应的设置窗口的表达式 菜单中选择它们,或者简单地输入 ht.kxx(其中 ht 是用于该模型的固体传热接口的标签)。
结束语
在这篇文章中,我们介绍了 COMSOL Multiphysics 中包含的定义曲线坐标系的不同方法,以及在什么时候应该选择哪种方法。
综上所述,对于大多数应用,使用自适应方法可以得到最佳解,而且计算成本相对较低。扩散方法的计算成本更低,但适用于没有弯道或变化截面的简单几何形状。其他方法在特定的情况具有优势,对一些应用也很有意义。
-
-
-
-
优点:计算成本比流动方法低,比扩散方法能更好地表现中等程度的弯曲。
-
缺点:经常需要手动选择特征值,并不是在所有情况下都很稳健。
-
-
优点:稳健的方法,支持处理横截面变化和急剧弯曲的应用
-
如果您想自己动手尝试模拟文中介绍的碳纤维模型,请点击底部“阅读原文”获取教程模型。如果大家有相关问题,欢迎留言讨论。
文章来源:comsol
 2023年8月25日 16:35
2023年8月25日 16:35 的矢量场
。由于大多数应用需要归一化的矢量场,COMSOL Multiphysics 会自动除以
进行归一化处理。第二个矢量场可以手动指定,笛卡尔坐标通常是一个不错的选择。以此为起点,我们重建第二基矢
,确保它与
垂直,并被归一化处理。最后,这两个矢量的叉积得到第三基矢
。
进行计算,并将所有涉及不同坐标系的量转换到
坐标系。任意坐标系中,由矢量
给出的方向总是可以转换为笛卡尔坐标,如下所示:
曲线坐标系(箭头)、温度梯度(流线)和温度(表面)。
曲线坐标系(箭头),速度场(流线),和压力(表面)。
是矢量场,
是单位矩阵,
是特征值。
。在使用自适应方法之前,这种方法被用于模拟多匝线圈,因为它可以产生最佳的截面恒定流线密度。
曲线坐标系(箭头),线圈方向(灰色流线)和磁通密度(红色流线)。
扩散法:流线遵循”最短”路径。
自适应方法:均匀分布的流线。
弹性方法:流线倾向于在凸形弯道处积聚。
流动方法:流线倾向于在凸形弯道处积聚。
流线表示用曲线坐标接口得到的矢量场。






















