Exponential Moving Average 指数移动平均

本文展示了如何设置一个计算速度较快的3维标量物理场的滑动平均处理。

如何使用指数移动平均法（Exponential Moving Average）进行快速场平滑处理？

数学移动平均方法 

（field mean + Sliding Sample Window）

在工程中，经常需要在模拟过程中计算物理场的平均值。在Simcenter STAR-CCM+中，可以通过创建一个场均值监视器（Field Mean Monitor）来轻松实现这一目标，该监视器会以给定的频率对给定的物理场进行采样，并提供其平均值。在模拟开始时，流动通常不是完全物理的，也就是还没有发展起来，需要经过一段时间才能稳定下来。为了避免在这个初始阶段对流场进行采样，可以使用Field Mean Monitor的Start选项，指示Simcenter STAR-CCM+仅在经过一定数量的迭代或时间步数后才开始采样物理场数据。如果使用Stop选项，则可以定义一个特定的窗口进行平均，可以指定采样数据的开始和停止的范围。

然而，有时候流动达到统计稳定并准备好进行有效采样的时间事先是未知的。或者，平均值可能被用作平滑短期波动的一种方式，同时保持对固有非稳定性的跟踪。在这种情况下，可以通过勾选启用滑动采样窗口选项并指定一个作为保留样本数量的窗口大小来使用Field Mean Monitor的滑动窗口功能（Sliding Sample Window）。

然而，这种方法存在一个主要缺点，即为了计算仅包括最近N个时间步样本的平均值，必须存储所有最近N个时间步的物理场数据。这意味着计算成本随着N的增加而增加，特别是内存需求（包括RAM和保存.sim文件的磁盘空间）随着N和体网格大小的增加而增加。对于大窗口采样平均的N和大网格模型，内存成本可能是不可接受的。

Exponential Moving Average

指数移动平均

当使用具有大小为N的滑动窗口的Field Mean Monitor时，最新时间步n处的移动平均值（Moving Average）MA的值计算如下。

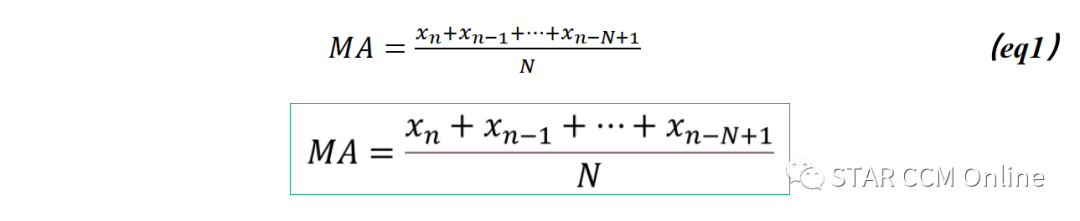
这意味着在这个平均值中，最近的N个时间步样本被等权重地加权为1/N，每个时间步的样子的加权因子相等，而N个时间步骤之前的样本被舍弃，即加权为0。比如，让N=10，且当前计算到了第99个时间步，那么第90个时间步之前的所有时间步的样本都对这个移动平均MA没有任何影响。

这种类型的平均值是众所周知的，其意义很容易理解。然而，该平均值的严格数学属性可能并不重要，对于特定的流程情况，其他类型的样本加权可能更合适。

指数移动平均法的定义如下：

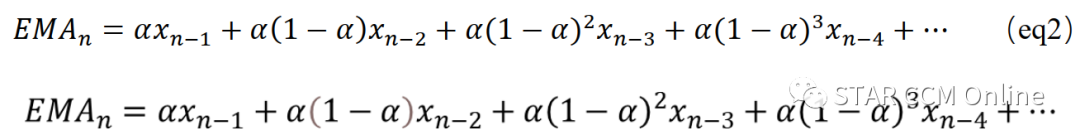
其中α是介于0和1之间的平滑因子。在这种平均中，之前的样本永远不会完全被舍弃，而是用指数衰减的权重加权。

• α越大，之前的样本变得可以忽略的速度越快，平滑效果越小，类似于具有较小窗口大小的N（相对于数学平均的滑动窗口采样）。

• α越小，一个样本对平均值的影响越长，平滑效果越大，类似于具有较大窗口大小N（相对于数学平均的滑动窗口采样）。。

从下面的图我们可以看到每种平均方法在不同窗口大小（N值）和相应平滑因子下α的响应情况：

根据（eq2），我们分别列出 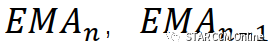的展开式：

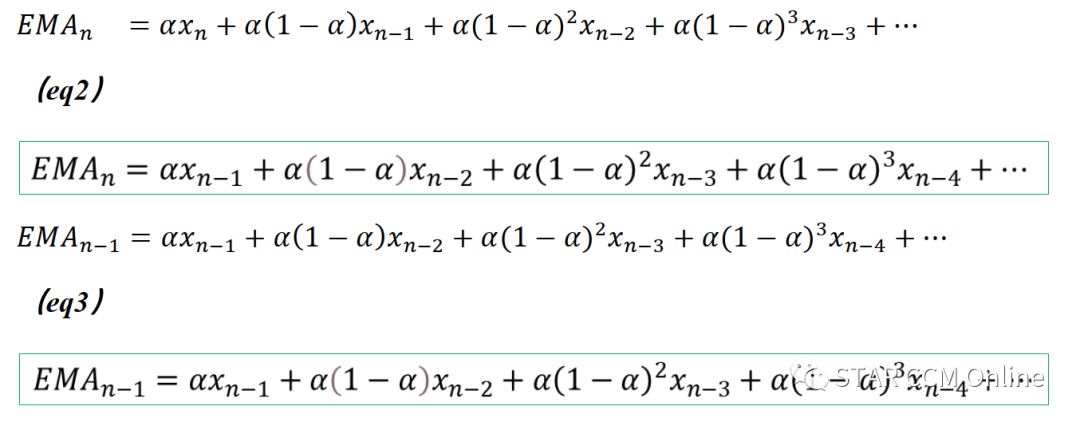
将（eq3）两边都乘以 得到：

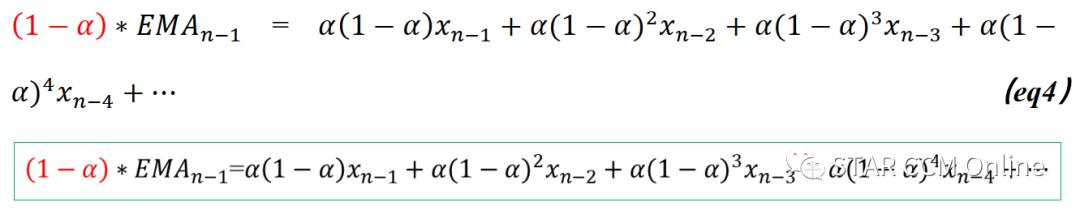
（eq4）的右边就等于（eq2）的右边第二项及以后所有项的和；这样（eq2）就可以写成：

指数移动平均法的 优点从（eq5）可以看出：只需要知道 当前时间步物理场x_n和 上一个时间步的平均值EMA_n-1，也就是只需要额外存储上一个迭代时间步的数据。相对于数学平均方法而言，保存N个时间步的物理场x_n-1、x_n-2、x_n-3---等，这可以节省大量的内存。（x_n中，x表示某个要进行平均的物理量，比如压力，温度等，n表示的当前时间步，n-1表示前一个时间步，n-2表示往前第2个时间步，n-3 ---依次类推）

指数移动平均法的实现

为了在STAR-CCM+中实现物理场的高效移动平均，可以参考下面步骤。

• 首先，创建一个新的物理场函数field function，比如将其重命名为EMA。

先暂时将其定义为空，也就是先让其空着，因为需要用到其自己在上一个迭代步中自己的值，而此时还不可用。

• 创建一个包含上一个时间步骤EMA值的监测函数。

通过STAR-CCM+软件的Monitor节点，新建一个Field Mean，这里取名为EMA_previous，激活Enable Sliding Sample Window，并将其值设定为1.这个定义的EMA_previous monitor将会在软件中表征为 ${EMA_previousMonitor}场函数，可以被引用或进行云图显示。也可以再另外定义一个新的场函数field function ,来直接引用这个EMA_previous monitor，如下图。

请注意，该方法仅适用于非稳态模拟，以获取以前时间步的物理场值，但无法获取以前迭代次的物理场值（相对于稳态分析而言）。

• 定义一个全局参数Parameter,在Tool-Parameter节点进行新建。用于定义前面提及的平滑因子α。

这里创建一个新的标量参数alpha，用于保存平滑因子的值。将其值设置为介于0和1之间的所需水平，以提供与具有窗口大小N的等权重移动平均值相对相似的行为。比如要达到与数学移动平均，取N=10滑动采样，相接近的数值，可以参考下面公式进行计算。α=2/(10+1)=~0.18。

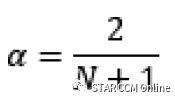
• 返回去补充定义EMA场函数。（这里假定对 压力进行采样）

参考（eq3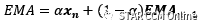） 定义：

${alpha}*${Pressure} + (1-${alpha}) * ${EMA_previous}

• 后续就可以使用这个EMA指数移动平均场函数了。

案例：MA与EMA的比较

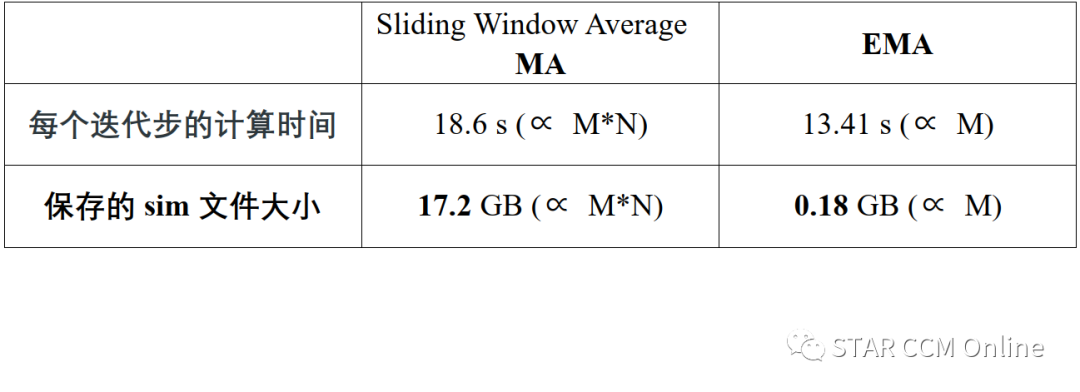
这里以一个圆柱绕流案例，体网格1M，数学移动平均中N取4000，每4000个时间步做物理量数值平均，比较了MA与EMA的计算效率与存储文件大小。供参考。

文章来源：STAR-CCM-Online