Matlab实现关联分析和优势分析

1、关联分析

现实中事物的联系很复杂，我们往往就需要对系统分析，哪些因素对他影响较大，那些较小，所以就会用到关联性分析。

以下面一个例子来介绍怎么做

x1 = [45.8 43.4 42.3 41.9];

x2 = [39.1 41.6 43.9 44.9];

x3 = [3.4 3.3 3.5 3.5];

x4 = [6.7 6.8 5.4 4.7];

求x2,x3,x4与x1的关联性，并确定谁与x1的关联性最强

x = [x1;x2;x3;x4];%将数据组成数据矩阵

首先就是标准化数据也叫初值化数据即xi（k）/xi（1）；

for i = 1:4

x(i,:) = x(i,:)/x(i,1);

end

data = x; %标准化之后的数据

上面每一个数据有4个观测时刻

n = size(data,2);

这样就求出了观测时刻的个数。

接下来就是求各比较数据与参考数据的关系

ck = data(1,:);%提出参考列

bj = data(2:end,:);%提出比较列

m2 = size(bj,1);%求比较数列的个数，即行数

t = zeros(size(bj));

for j = 1:m2

t(j,:) = bj(j,:) - ck;%相当于x0(t)-xs（t）

end

然后就是求关联系数了

mn = min(min(abs(t')));%求最小差

mx = max(max(abs(t')));%求最大差

rho = 0.5;%分辨系数设置

ksi = (mn+rho*mx)./(abs(t)+rho*mx);%求关联系数

最后就是求关联度和进行关联度排名了

r = sum(ksi,2)/n;%求关联度

[rs,rind] = sort(r,'descend')%对关联度进行排序

运行结果为：

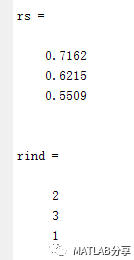
rs代表关联度从大到小排序，rind代表对应的x的序号。可以看出x2以x1的关联性是最大的。

代码为

2、优势分析

优势分析就是当目标数列不止一个，与目标数列相关的因素也不止一个时，为了判断那个因素的影响较大，就会进行优势分析。假如有m个目标，记为y1，y2,...，ym。再假设有l个因素，记为x1,x2,…,xl。显然每一个目标对l个因素就有l个关联度。设rij表示相关因素xj对目标yi的关联度，可构造关联（度）矩阵R=(rij)mxl

下面以一个例子来说明

下面为目标数列

y1 = [170 174 197 216.4 235.8];

y2 = [57.55 71.74 76.8 80.7 89.85];

y3 = [68.56 70 85.38 99.83 103.4];

下面为因素数列

x1 = [308.58 310 295 346 367];

x2 = [195.4 189.9 189.2 205 222.7];

x3 = [24.6 21 12.2 15.1 14.57];

x4 = [20 25.6 23.3 29.2 30];

x5 = [18.98 19 22.3 23.5 27.66];

通过分析得到关联度矩阵R为

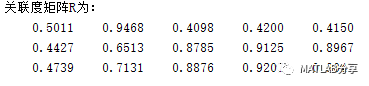
可以看出最大的数为0.9468，说明x2对y1的影响较大。

具体代码为

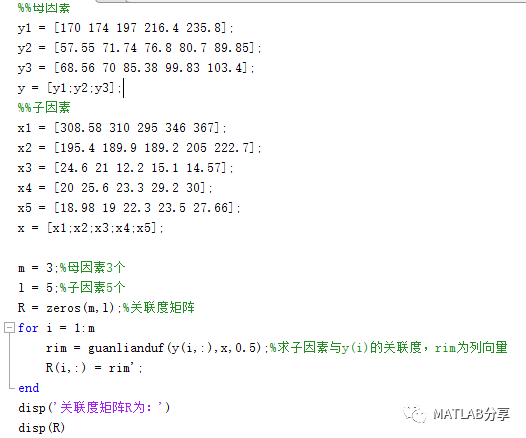
优势分析代码中求关联度的函数为根据上述求关联度代码改编成关联度函数。

文章来源：matlab分享