简述极端变形问题的数值模拟

一、引言

极端变形问题是一类几何、材料和边界条件均为非线性的复杂问题。典型的极端变形问题通常有：超高速碰撞、冲击爆炸、金属加工成型、边坡失效、液体晃动等等。

小到踩扁一个易拉罐、射穿一块玻璃，大到飞机坠落、天体撞击，许多极端变形问题中的断、裂、破、碎等现象往往会引发灾难性的后果。

极端变形问题示例

不难想象，对于被踩扁的易拉罐而言，这无疑是一场“灭顶之灾”。若想借助数值模拟技术来分析极端变形问题，究竟有哪些难点？

二、模拟方法

难不难取决于采用什么模拟方法。目前较为成熟的模拟方法有以下几种：Lagrange（拉格朗日）格式有限元法、Euler（欧拉）法、ALE（任意拉格朗日-欧拉）方法、SPH粒子法等等，当然还有我们今天的主角物质点方法（Material Point Method, MPM）。

先说结论：MPM特别适合极端变形工况的分析，用了它，就不难。下面我们分别来介绍。

Lagrange（拉格朗日）格式有限元法，其单元与材料固连，可以准确跟踪材料界面、追踪材料内部的变形历史，具有较高的模拟精度。然而，极端变形问题往往伴随着局部单元的严重畸变，而Lagrange模型的求解十分依赖于单元形状的规则程度，越畸形的单元其求解精度越低，甚至无法继续计算下去。通常可由如下雅可比矩阵J来描述等参变换过程中从参考坐标系到实际坐标系的映射关系：

若单元变形较大导致网格发生严重畸变，则上述矩阵的行列式（det J）可能接近零甚至为负，说明此时单元已经失效，无法正确描述变形行为。所以，传统Lagrange方法的痛点之一在于单元畸变。

det J 为正（左）、为零（中）、为负（右）

Euler（欧拉）法将固定的空间网格作为参考框架，令材料在网格之间流动。由于网格固定所以天然规避了Lagrange方法的单元畸变困难，适于分析流动问题。但是，其网格与材料独立，不易准确跟踪材料界面，难以引入与变形历史相关的材料模型，且非线性对流项也会导致数值求解困难。

ALE（Arbitrary Lagrangian-Eulerian）方法全称是任意拉格朗日-欧拉方法，是一种综合了拉格朗日和欧拉描述的计算方法，其计算网格可以独立于物质坐标系和空间坐标系运动，通过规定合适的网格运动形式可以准确地描述物体的移动界面，并维持单元的合理形状。但是，类似于欧拉法，在ALE方法的控制方程中仍会出现对流项，使得系数矩阵不对称，并可能得到振荡解，需要进行相当细致的数值处理。

区别于上述的几种有网格方法，极端变形问题的另一类解决方法是无网格法，比较具有代表性的方法是SPH粒子法，在很多CAE软件中已经具备。SPH方法的核心思想是将连续介质离散为质点（粒子）集合，每个粒子都带有一定的物理量（如质量、密度、速度等），通过计算这些粒子的相互作用，可以更新力学系统的运动状态。相比传统的有限元方法和有限体积方法，SPH方法适于处理自由表面流动和大变形问题，因为它不需要网格，可以自适应地描述固体材料、流体物质的大变形。然而，传统SPH方法存在着拉力不稳定、邻近粒子搜索、边界施加困难等问题，其精度和稳定性较难控制，并且SPH方法对计算资源需求通常较其它方法更高。

那么对于极端变形问题，到底有没有一种方法既能解决Lagrangian有限元计算中存在的网格畸变问题，又可以改善Euler方法中运动表面的跟踪困难，还能够比SPH节省计算资源、具备更高的计算效率呢？

答案就是物质点方法（Material Point Method, MPM）。

三、物质点法

MPM是上世纪90年代提出的数值方法，它采用拉格朗日质点和欧拉网格的双重描述。相比Lagrangian有限元计算中介质被离散为连续单元的方法，物质点方法中把物体离散为带有质量的物质点。

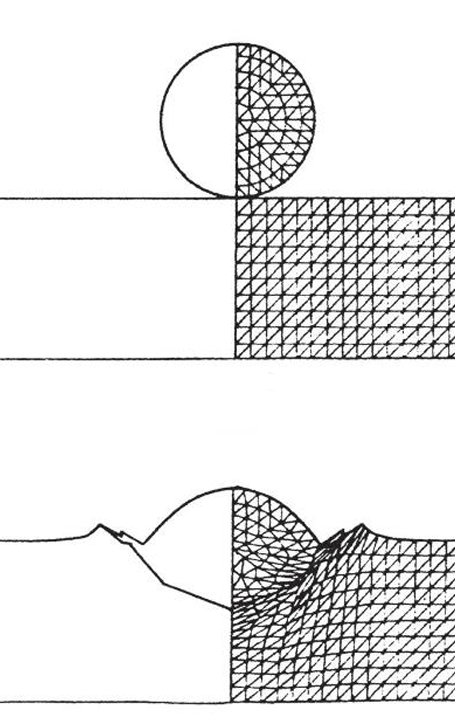
有限元方法求解侵彻问题实例

物质点方法求解落锤强夯示例

计算过程中，物质点携带了全部的物质信息，通过将这些物质信息（质量、动量、力等）映射到背景网格，在背景网格上求解动量方程即可得到速度变化量和位置变化量，将这些信息再映射回物质点，即可更新物质点的速度和位置。

由于背景网格本身不携带任何物质信息，且物质点和背景网格之间也没有相对运动，这就避免了欧拉法中的对流项的计算，而且容易跟踪物质界面，同时由于物质点携带了完整的物质信息，每次更新完状态后就可以抛弃变形后的背景网格，避免了网格畸变问题的产生，实际的计算效率更高。

物质点方法综合了拉格朗日法和欧拉法的优点，能够很好的处理极端变形问题，例如冲击侵彻、爆炸损伤、断裂破碎、流固耦合等涉及结构和材料极端变形模拟；而对于小变形假设的静力、拟静力或低速动力学问题，相同插值阶次的物质点法在计算精度上低于传统有限元方法。因此，针对这类问题，采用有限元方法更合适。

四、案例介绍

物质点方法到底好不好用，相信大家通过上述理论知识已有初步了解。而该方法在实际应用中能否有效解决问题，我们不妨从以下几个案例中寻找答案。顺便不经意地透露一下，本次仿真计算采用的工具为云道智造开发的Simdroid-MPM3D，在兼顾效率与精度的同时，还兼备易学易用的特性，文末提供试用版本下载链接。

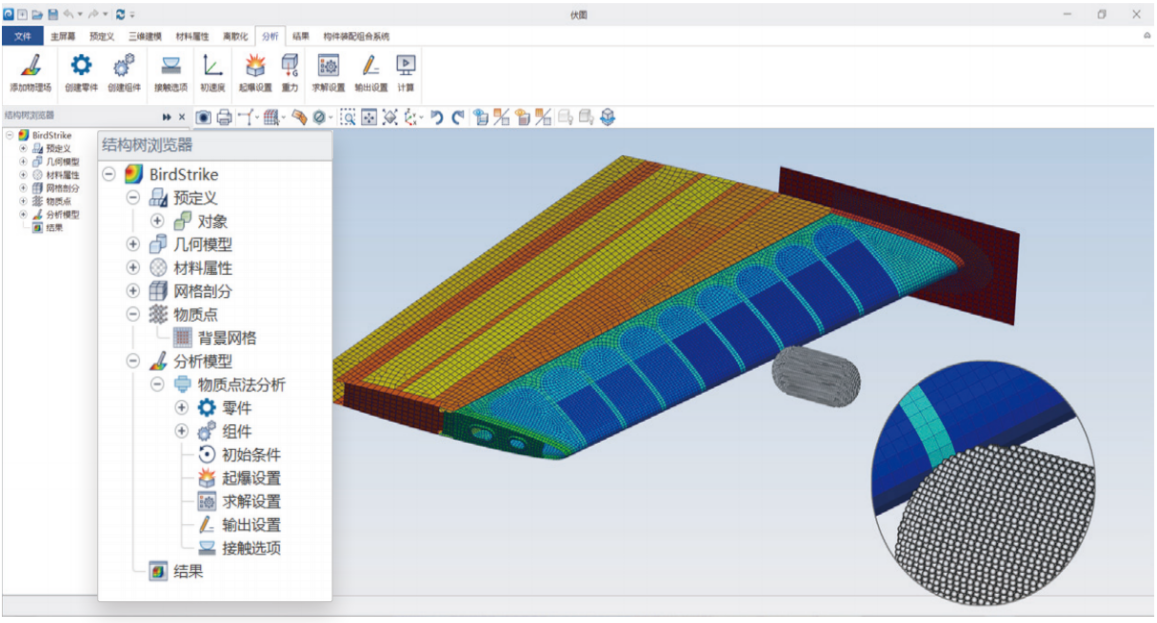
Simdroid-MPM3D主界面

首先给大家介绍典型的极端变形案例：超高速撞击。铅球以6.58km/s的速度撞击6.35mm厚的靶板，左图是试验结果，右图是数值模拟结果。可以看到，物质点法正确的模拟了打穿靶板之后的碎片云形貌，模拟结果的精度与试验现象吻合较好。

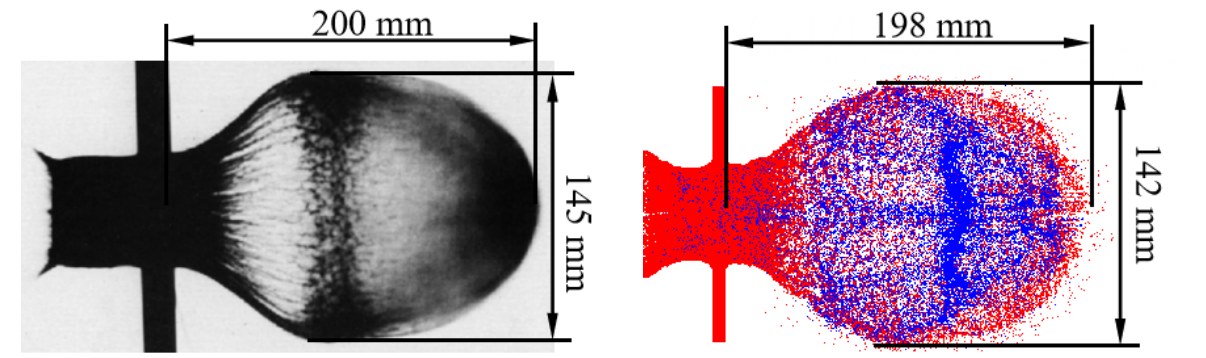
超高速撞击的仿真与实验结果对比

然后是卵形体侵彻钢筋混凝土的案例，该问题仿真的难点在于钢筋（有限元单元）和混凝土（物质点粒子）之间的耦合算法，且需同时模拟钢筋的断裂和混凝土的破碎。

下图所示的射流侵彻岩层导致的岩体破碎与裂纹扩展过程也是极端变形的仿真应用案例。

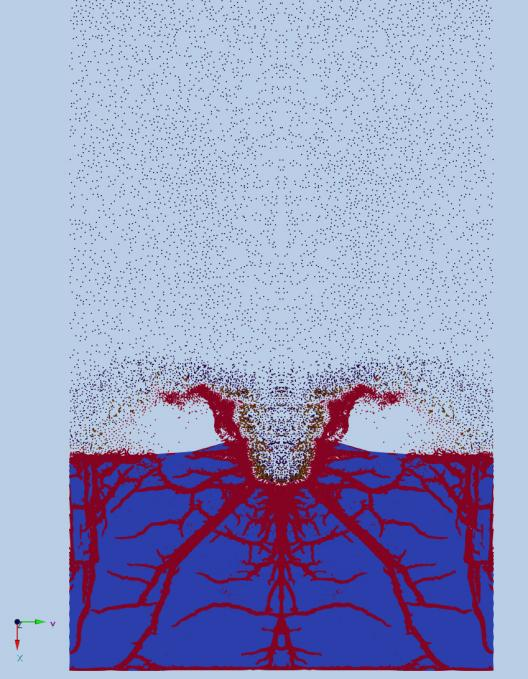
五、结束语

极端变形问题的仿真对于工程实践和科学研究具有重要意义。尽管这类问题的仿真模拟通常被认为难以执行，但是随着Simdroid-MPM3D软件的推出，该困局将会改观。申请试用Simdroid-MPM3D