四节点/八节点四边形单元悬臂梁的Matlab有限元编程——《Matlab有限元编程从入门到精通》系列
 2022年10月11日 19:10
2022年10月11日 19:10导读:大家好,我是SimPC博士,主要从事工程结构抗震及减隔震研究,玻璃成型热工设备流动及传热研究,玻璃材料力学性能研究。精通有限元等数值算法的实现,有限元软件二次开发,数据处理,偏微分方程求解,优化算法,GUI界面开发等。有多项科研成果,其中SCI论文4篇,EI3篇,专利2篇。
本文的案例主要以受均布荷载和集中荷载的变截面悬臂梁为研究对象,通过matlab编制四节点和八节点四边形单元有限元程序来对悬臂梁进行受力分析,提供对应有限元基本理论讲解的同时展示相应代码的实现技巧。
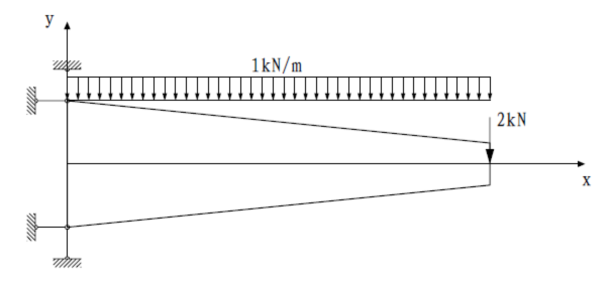
几何域离散,获得标准化的单元;
通过能量原理(虚功原理或最小势能原理,获得单元刚度方程;
单元的集成(装配);
处理位移边界条件;
计算支反力;
计算单元的其他物理量(应力应变)。
节点描述
场描述
-
单元刚度方程。
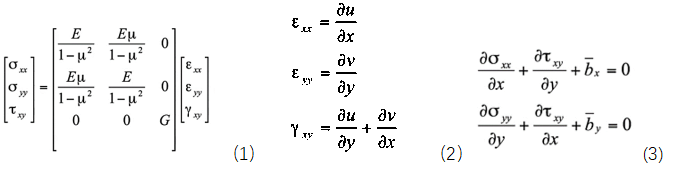
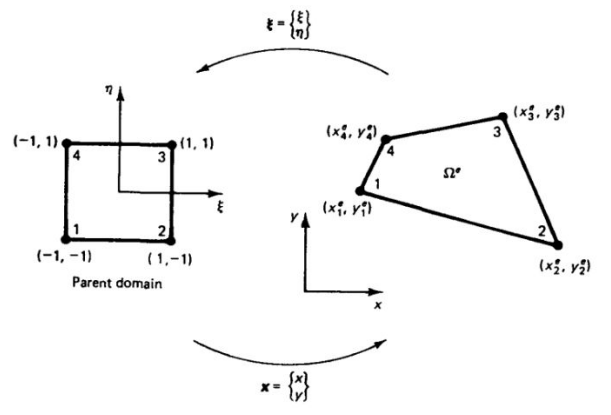
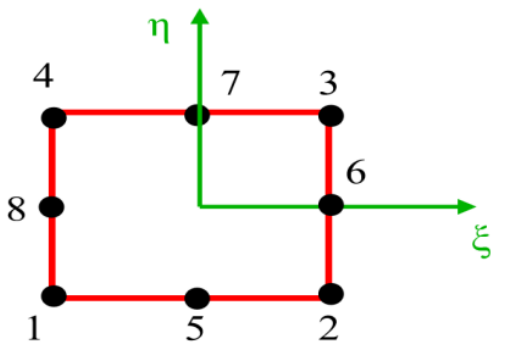
图2-1 平面四节点矩形单元的映射关系
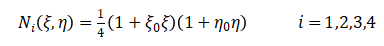 (4)
(4)
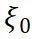 和
和
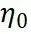 为自然坐标系下的节点坐标值。
为自然坐标系下的节点坐标值。

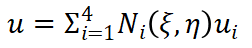 (7)
(7)
function N=ShapeFun(s,t) N1=1/4*(1-s)*(1-t);N2=1/4*(1 s)*(1-t);N3=1/4*(1 s)*(1 t);N4=1/4*(1-s)*(1 t);N=[N1 0 N2 0 N3 0 N4 0;0 N1 0 N2 0 N3 0 N4];end
同理平面八节点矩形单元如图2-3所示,单元共有8个节点,16个自由度。单元的形函数定义如下:
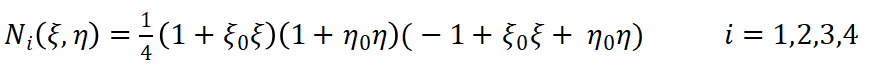 (8)
(8)
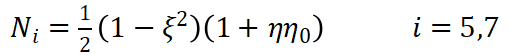 (9)
(9)
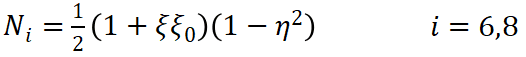 (10)
(10)
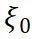 和
和
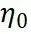 为自然坐标系下的节点坐标值。
为自然坐标系下的节点坐标值。
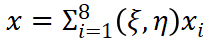 (11)
(11)
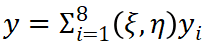 (12)
(12)
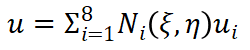 (13)
(13)
function N=ShapeFun(s,t) %% 四边形八结点等参单元形函数矩阵 % 角点N1=1/4*(1-s)*(1 t)*(-s t-1); N2=1/4*(1-s)*(1-t)*(-s-t-1); N3=1/4*(1 s)*(1-t)*(s-t-1); N4=1/4*(1 s)*(1 t)*(s t-1); % 边中点 N5=1/2*(1-t^2)*(1-s); N7=1/2*(1-t^2)*(1 s); N6=1/2*(1-s^2)*(1-t); N8=1/2*(1-s^2)*(1 t); N=[N1 0 N2 0 N3 0 N4 0 N5 0 N6 0 N7 0 N8 0;0 N1 0 N2 0 N3 0 N4 0 N5 0 N6 0 N7 0 N8];
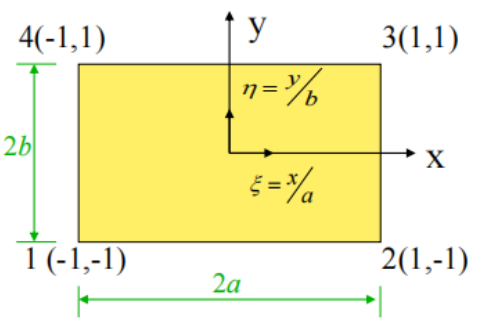
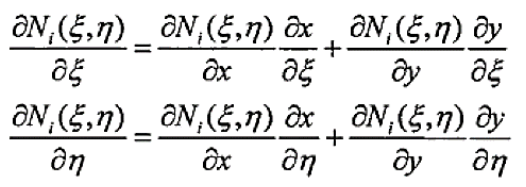 (14)
(14)
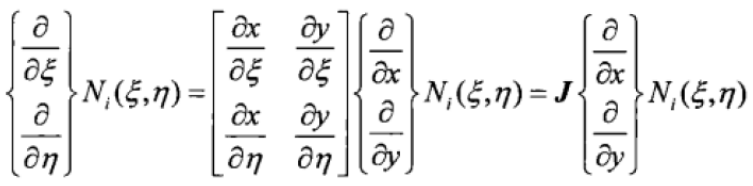 (15)
(15)
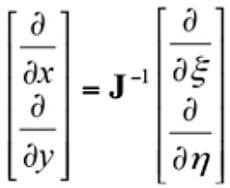 (16)
(16)
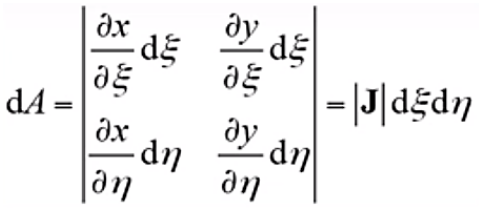 (17)
(17)
 (18)
(18)
function J=Jacobi(ie,s,t,Elements,Nodes) ENodes = Elements(ie,:); %获取单元结点 xe = Nodes(ENodes(:),:); %获取节点坐标 x1=xe(1,1);y1=xe(1,2); x2=xe(2,1);y2=xe(2,2); x3=xe(3,1);y3=xe(3,2); x4=xe(4,1);y4=xe(4,2); J=1/4*[-(1 t) -(1-t) 1-t 1 t;1-s -(1-s) -(1 s) 1 s]*[x1 y1;x2 y2;x3 y3;x4 y4];end
function J=Jacobi(ie,kesi,yita,Elements,Nodes) ENodes = Elements(ie,:); %获取单元结点 xe = Nodes(ENodes(:),:); %获取结点坐标 x1=xe(1,1);y1=xe(1,2); x2=xe(2,1);y2=xe(2,2); x3=xe(3,1);y3=xe(3,2); x4=xe(4,1);y4=xe(4,2); J=1/4*[-(1-yita),(1-yita),(1 yita),-(1 yita);-(1-kesi),-(1 kesi),(1 kesi),(1-kesi)]*[x1 y1;x2 y2;x3 y3;x4 y4];end
为了求出上述平面四节点和八节点单元的单元刚度矩阵,需要借助能量原理(虚功原理、最小势能原理)进行推导,能量原理的推导过程大家可以参考任意一本有限元理论书籍,都会有详细的推导过程,这里就不做进一步推导讲解,直接给出物理坐标和几何坐标系下的刚度矩阵的公式
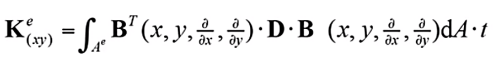 (19)
(19)
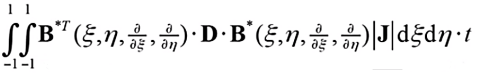 (20)
(20)
其中B矩阵为应变矩阵,如下式;D矩阵为材料刚度矩阵,如公式(1)所示,是物理方程中表征应力应变关系的矩阵。从上述刚度矩阵的表达式可以看出,自然坐标和物理坐标间要完成坐标映射、偏导映射、面积隐射三个部分,具体映射公式已在上一节的等参单元讲解中详细给出。
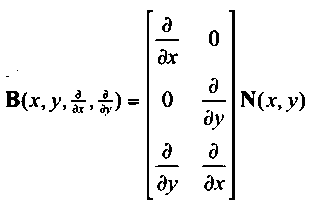 (21)
(21)
4、高斯积分
公式(20)中的单元刚度矩阵通过数值积分求得,本案例中的四节点和八节点四边形等参单元均采用2*2个积分点的高斯积分即可求得精确结果。高斯积分点的坐标具体如图所示。
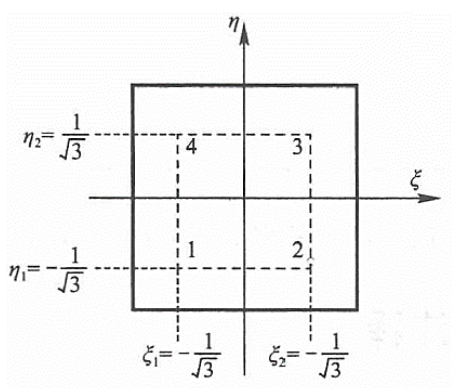
4-1 Gauss积分点示意图
公式(20)写成数值积分的形式为
 (22)
(22)
对于8节点单元实现上述数值积分的代码如下所示:
r = [-sqrt(1/3) sqrt(1/3)]; % 2*2 高斯积分点 s = [r(1) r(1) r(2) r(2)]; t = [r(2) r(1) r(1) r(2)]; % 高斯积分点坐标for i=1:4 J = Jacobi(E_ID,s(i),t(i),Elements,Nodes); % 雅可比矩阵 Nst = DiffShapeFun(s(i),t(i)); % 形函数关于自然坐标s,t求导 Nxy = zeros(8,2); for j=1:8 Nxy(j,:) = (J\Nst(j,:)')'; % 形函数关于 x,y 求导=inv(J)*Nst end Bm = [Nxy(1,1) 0 Nxy(2,1) 0 Nxy(3,1) 0 Nxy(4,1) 0 Nxy(5,1) 0 Nxy(6,1) 0 Nxy(7,1) 0 Nxy(8,1) 0; 0 Nxy(1,2) 0 Nxy(2,2) 0 Nxy(3,2) 0 Nxy(4,2) 0 Nxy(5,2) 0 Nxy(6,2) 0 Nxy(7,2) 0 Nxy(8,2); Nxy(1,2) Nxy(1,1) Nxy(2,2) Nxy(2,1) Nxy(3,2) Nxy(3,1) Nxy(4,2) Nxy(4,1) Nxy(5,2) Nxy(5,1) Nxy(6,2) Nxy(6,1) Nxy(7,2) Nxy(7,1) Nxy(8,2) Nxy(8,1)]; ke = ke det(J)*Bm'*D*Bm*Width; %数值积分 end
5、均布荷载的施加
在有限元中分布力要转为等效节点荷载,而确定等效节点荷载的方法也是通过能量原理推导得到
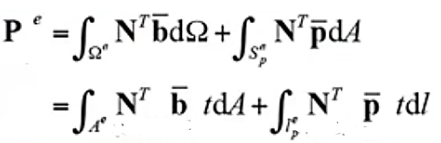 (22)
(22)
上式中,第一项代表体积力的等效荷载,第二项代表面积力的等效荷载,这个案例我们只考虑面力荷载。实现公式22的代码为
function Pe=UniLoad(ie,N_ID_p1,q0,Nodes,Elements) k=-0.625e-3; % 均布荷载值 N/mms = [-sqrt(1/3) sqrt(1/3)]; % 2*2 高斯积分点ENodes = N_ID_p1(ie,:); %获取单元结点号Pe=zeros(16,1); %生成临时单元节点力零列向量x1=Nodes(ENodes(1),1);x6=Nodes(ENodes(4),1);L16=abs(x6-x1); %单元长度for i=1:2 %用于高斯积分的求和循环 N_q=ShapeFun(s(i),1); % 4级子程序:ShapeFun(s(i),1) q_x=q0; Pe=Pe N_q'*q_x*[0;L16/2]; endend
三、Matlab有限元编程精品课
网格划分及变形结果如图3-1所示。本案例的详细视频教程和对应的matlab源码,请关注我的技术邻官网和APP精品课程《Matlab有限元编程从入门到精通10讲》,点击试看《Matlab有限元编程从入门到精通》。

图3-1 梁变形结果
此外,为帮助大家更好的入门学习Matlab有限元编程分析能力,笔者准备了了一些有限元编程书籍资料供大家下载。欢迎大家直接在附件下载。另外本人推出《Matlab有限元编程从入门到精通》视频教学课程。点击试看《Matlab有限元编程从入门到精通》。
本课程为matlab有限元编程专题课,课程主要以案例的形式进行讲解,中间会穿插案例中所涉及到的有限元基本理论,案例不局限于力学问题的有限元求解,还会涉及传热学、电学等问题的有限元求解。
因为固体力学领域我最熟悉,所以我们从固体力学开始,所涉及的单元有杆单元,梁单元,平面三角形单元,薄板单元,厚板单元,四面体实体单元等等,力学问题有静力学问题,也有动力学问题,后期还会涉及材料非线性、几何非线性、接触非线性等非线性问题,内容丰富,不断更新完善。
此外,笔者为所有订阅用户提供知识圈答疑服务和VIP用户交流群。并附赠课程相关资料等(平台支持自行开具电子发票)。
-
快速获得各典型有限元案例的 Matlab代码; -
学习并掌握有限元基础理论; -
掌握Matlab编程实现有限元算法的流程; -
掌握多种有限元单元的基本理论Matlab编程实现过程; -
掌握静力学、动力学、材料非线性、几何非线性、接触非线性问题的Matlab编程实现; 为订阅用户提供知识圈答疑服务,并建立VIP用户交流群,后续可根据订阅用户需求进行加餐直播。此外还提供课程对应的学习资料模型一份。
理工科院校学生和教师;
学习型仿真设计工程师;
Matlab有限元编程兴趣爱好者和应用者。

工程师必备
- 项目客服
- 培训客服
- 平台客服
TOP





















