有限元学习日记(持续更新)
欢迎大家关注我,会不定期在这篇文章后中更新有限元相关的知识
有限元分析通用标准
此标准包含了一些基础术语、有限元分析注意事项等,对于新手来说有很重要的参考意义。并且由于是国标所以专业性上有保障。
2.壳单元的正反
一般来说不涉及到接触时不用太过在意壳单元的正反,当两个壳单元接触时尽量保持正对正、反对反,这样容易收敛。
3.网格质量控制(参考 有限元网格剖分与网格质量判定指标 李海峰1;吴冀川2;刘建波1;梁宇兵1)
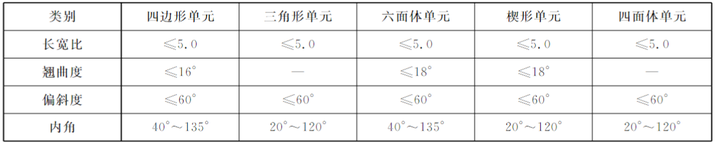
网格质量对于最终的有限元计算结果影响很大,但是对于不同的分析类型、不同关注部位、不同求解器来说网格质量标准会不同,并且对于网格质量的衡量标准有很多。下面大概姐介绍一些常用的,并给出最常用参数的常用标准,仅供大家参考,还是用根据具体情况自行选择。
对于三角形单元常检查:单元长度(最小、最大)、长宽比、扭曲角和内角大小
对于四边形网格主要检查:单元长度、长宽比、翘曲度、雅可比、弦偏离度
1.长宽比
单元最长边与最短边之比(二维与三维网格的计算方式不同,具体参考使用的软件的帮助文档)
2.翘曲度
四边形单元翘曲角。该指标表征了单元 在单元的面外的翘曲程度,面外翘曲发生在单元 面的节点不共面的时候。其定义如下:依次沿对 角线将四边形分为两个三角形,寻找这两个三角 形所在面构成夹角的最大值,该角即为翘曲角。
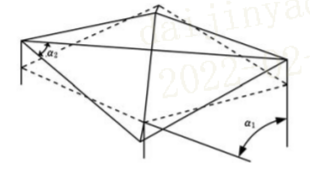
3.内角
即内角角度,常用于描述单元最大内角或最小内角。
4.扭曲角(偏斜度)
定义为:对边中点的连线的夹角的最小角的余角(注意是余角,不是夹角本身)。还有另外一种定义:单元相邻边夹角与60度/90度的差值(三角形单元为60度,四边形单元为90度)

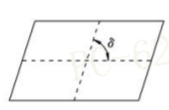
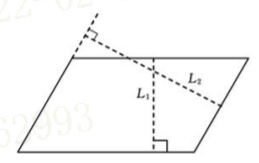
5.弦偏离度
单元各边中点与各点在对 应边上的投影点的距离值,见下图中的L1、L2
4.屈服准则(参考 几种各向同性屈服准则的比较分析 李忱1, 赵丽2)
有五种屈服准则包括:Tresca屈服准则、Mises屈服准则、Hill屈服准则、Barlat-Lian屈服准则、Drucker-Prager屈服准则。
这里金属材料最常用的是Tresca与Mises屈服准则,也称为第三、第四强度理论。
Tresca屈服准则
1864年 Tresca提出了最大剪应力屈服准则,认为当受力物体(质点)中的最大切应力达到某一定值时,该物体就发生屈服.其数学表达式为:
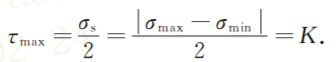
Mises屈服准则
1913年 Mises在研究了诸多实验结果后,提出了基于能量理论的 Mises屈服准则,认为在一定的变形条件下,当受力物体内一点的应力偏量的第二不变量J2 达到某一定值时,该点就进入塑形状态,其数学表达式为
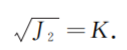
省略推导过程,最后可以写成
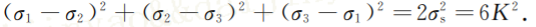
Mises屈服准则的物理意义为:在一定的变形 条件下,当材料的单位体积形状改变的弹性位能(又 称弹性形变能)达到某一常数时,材料就屈服。
后边几种屈服准则这里我不太常用就不过多介绍了
5.加工硬化(强化)
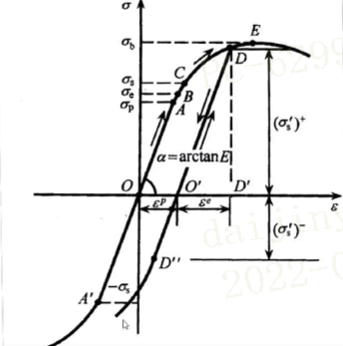
金属材料在再结晶温度以下塑性变形时强度和硬度升高,阻碍金属的进一步变形,而塑性和韧性降低的现象。又称冷作硬化。下面我们从材料的应力应变曲线来分析加工硬化的过程下图是常见钢铁材料的应力应变曲线有三个重要的拐点。可能有些教材还分了上屈服点与下屈服点。

弹性阶段
对物体施加外力,当物体最大应力小于弹性极限时,撤销外力,物体恢复原状。
塑性阶段
当金属所受应力超过材料的弹性极限,此时若撤销外力即会产生不可恢复的塑性变形,如下图所示。撤销外力时物体的应力应变会沿着变化。假设此时再施加载荷,物体的应力应变曲线会从沿着变化。只从图线上看材料的屈服点从原来的C点提高到了D点,材料得到了强化(许多教材硬化可能有点不合适,材料硬度并没有增强,是强度提高了),所以这种现象被称为加工硬化(强化)
6.reb2和rbe3单元的区别
rb就是rigid body的缩写,顾名思义就是模拟刚体。但是rbe2的从节点的运动与主节点完全相同,主要用于模拟刚性连接;而rbe3单元的主节点位移是众多从节点位移的平均值。
7.工程(名义)应力应变曲线与真实应力应变曲线
在实验测量材料的应力应变曲线时,需要使用如下图所示的仪器
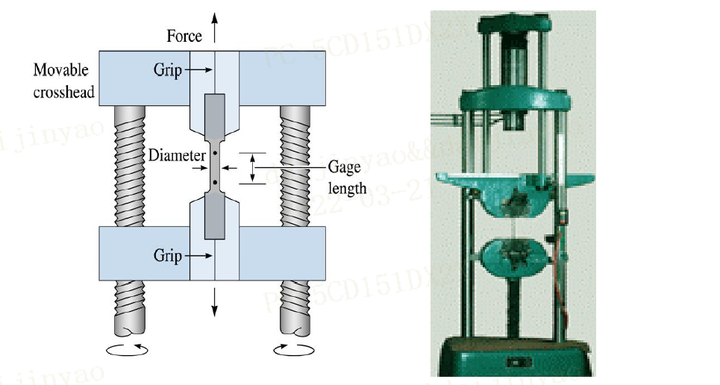
在对材料进行拉伸时,材料的截面会发生颈缩。如下图所示
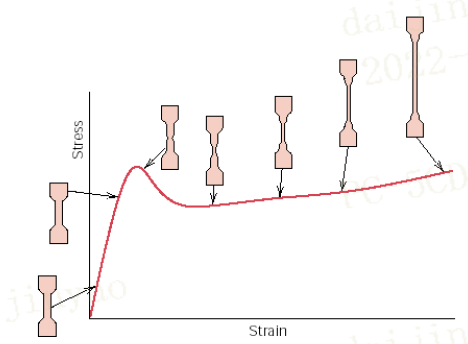
名义应力是指用是用施加的载荷F除以材料初始(未受力)时的截面积

名义应变是指用材料的的伸长量除以原始长度

但是我们需要的时发生变形那部分的材料的应力应变曲线,这样才能表征材料在受力状态下的属性。那么就需要用发生颈缩处的材料的应力与应变。这就引出了真实应力、应变的概念。
这里真实应变的推导就省略了(根本原理是材料的体积是一定的),真实应力很好理解就是用载荷除以受力后的截面积。具体公式如下
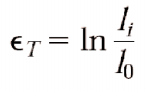
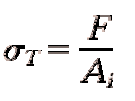
真实应力与应变和名义应力、应变之间的关系如下

8.模量
最常用的三种模量分别为弹性(杨氏)模量E、剪切模量G、体积模量K
弹性模量E是指材料在弹性变形范围内(即在比例极限内),作用于材料上的纵向应力与纵向应变的比例常数
剪切模量G是指剪切应力与剪切应变之比
体积模量K可描述均质各向同性固体的弹性,可表示为单位面积的力,表示不可压缩性,是所受压力变化与体积变化之比
这三者之间可以互相转化,关系如下,v为泊松比
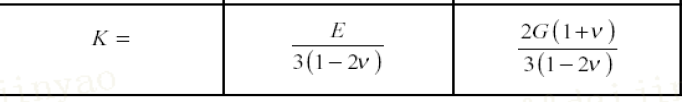
9.如何判断材料的屈服强度
拿到材料的真实应力应变曲线后应该如何判断材料的屈服强度呢
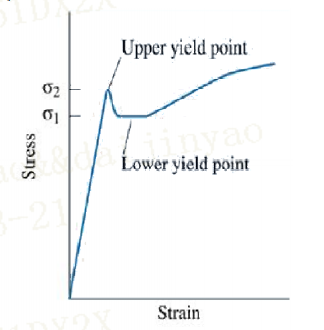
一般来说我们是选取材料发生明显屈服时的应力作为材料的屈服强度,下图中可以看到材料有一个很明显的屈服过程,这里将屈服点分为了上屈服点和下屈服点
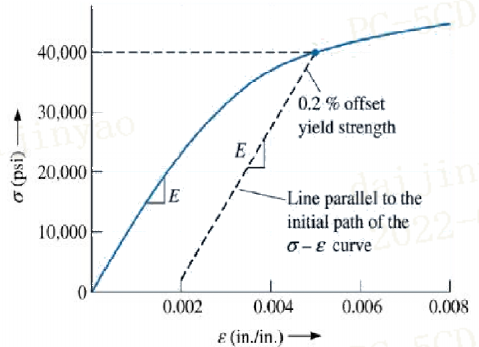
但是如下图这种没有明显屈服点的应力应变曲线,对于金属材料来说一般选取应变0.2%点做平行于弹性阶段的直线,与曲线相交的点处即为屈服强度
10.Abaqus中的接触详解
在有限元分析中线性模型的计算一般不会遇到收敛问题(除模型自身有问题),但是当遇到几何非线性、边界(接触)非线性、材料非线性时很容易出现不收敛的情况。其中接触非线性时以上三种非线性中最难理解、可调参数最多、最难收敛的情况。
这里只介绍Abaqus/Standard中的几种接触模型与相关原理设置。
接触的三因素为:
主从面确定
接触区域离散化
接触绑定
对用Abaqus/Standard通用接触来说,以上三种因素的参数都是由Abaqus默认选择的,无需用户关心。对于接触对来说我们就需要对以上三种因素中的参数进行设置,通常来说默认的设置可以满足大多数计算的收敛与计算精度。但是如果想提高计算精度或者遇到了收敛问题,以下的知识能够快速帮助你确定需要进行调整的参数。

1.接触绑定
接触绑定可以分为小滑移(small sliding)和有限滑移(finite sliding)。下面详细解释:
小滑移
小滑移中从面不可以穿透主面。主面和从面之间的网格不必匹配,但是如果主从面之间的网格相互匹配会提高计算的精度。对于主面和从面之间的网格不必匹配的情况,也可以通过调整初始接触的容差增加计算精度,因为大家使用的前处理软件各不相同,这里就直接说控制参数在Abaqus中的关键:“ADJUST”。
小滑移中假设主从面间的相对滑移移动小,允许主从面节点相对转动。软件会在初始判定接触时将一个从节点和一系列的主节点绑定(是的,你没看错,是一个从节点对应多个主节点)。至于具体绑定的方法与流程,大家参考帮助文档Abaqus Theory Guide (6.14),这里不做过多赘述。
有限滑移
有限滑移允许主从面之间出现相对转动以及滑移。这里注意,有限滑移允许的主从面相对滑移量要大于小滑移允许的滑移量。(PS.一直觉得这两个名称傻傻分不清楚,应该叫小滑移、大滑移比较贴切)。具体的绑定方法与流程参考帮助文档Abaqus Theory Guide (6.14)。
2.接触区域离散化
分为点面接触与面面接触
点面接触
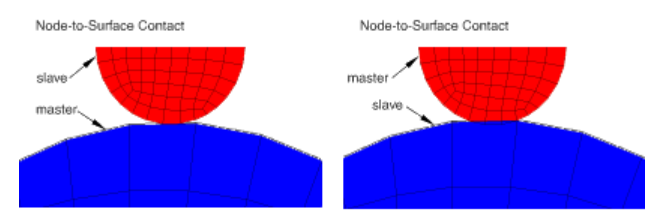
这种接触算法不允许从面穿透主面,允许主面穿透从面。就像下图所示,如果从面网格较密、主面网格较疏,就会造成右图中的情况,实际结果为该部位不会差生应力或者产生的应力远小于实际接触产生的应力。
因此我们在使用NodeToSurface时尽量保证从面的网格节点密度比主面更密。
每一个从点投影到主面,通过计算距离确定与该从点关联的主面节点(也就是说一个从节点可能对应多个主节点)。
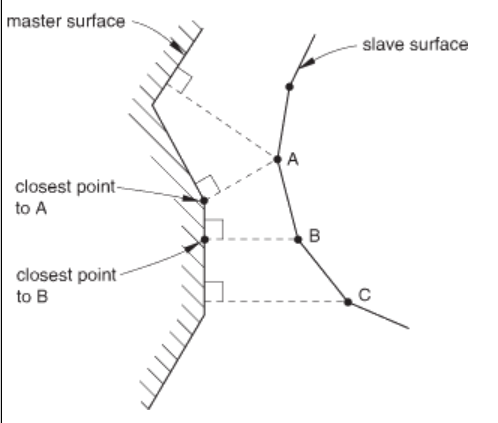
当然点面耐久中的点不仅仅可以是网格节点上的点,实际上我们在进行一些边和面接触(例如刀且肉)时也可以使用点面接触。(以下为帮助文档原话:The only information needed for the slave surface is the location and surface area associated with each node; the direction of the slave surface normal and slave surface curvature are not relevant. Thus, the slave surface can be defined as a group of nodes—a node-based surface.)
面面接触
面面接触中不是根据单个从节点来确定主从面的接触,而是根据一个以从节点为中心(大致)的一定区域的从节点。
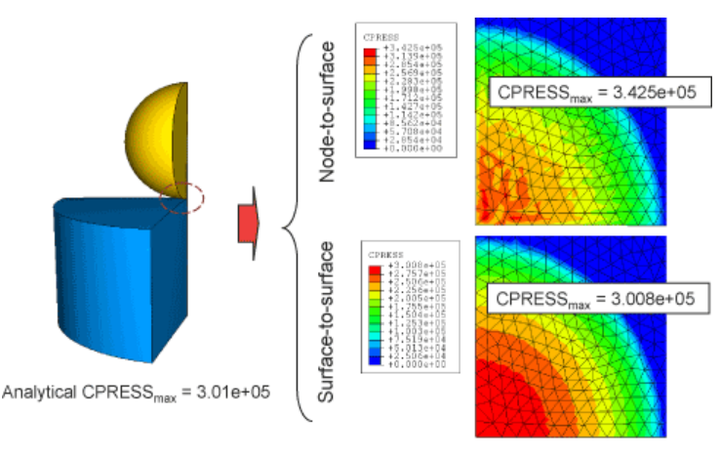
面面接触也不允许从面穿透主面。但是与点面接触不同的是,面面接触中从面节点的一定区域不允许穿透主面,而点面接触时从面节点不允许穿透主面。因此点面接触相对从面接触在面上的应力分布呈现波峰、波谷的形状,从下面的图中可以很清晰的看出。随着网格的细化点面接触这种情况会逐渐消失,但是会与相同的网格尺寸来说面面接触往往比点面接触的结果更加贴合实际。
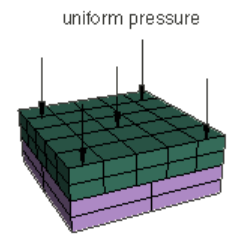
给大家再举一个例子,两个板接触,约束底部、顶部施加100Pa压强,两个板接触面的接触应力也应该是100Pa
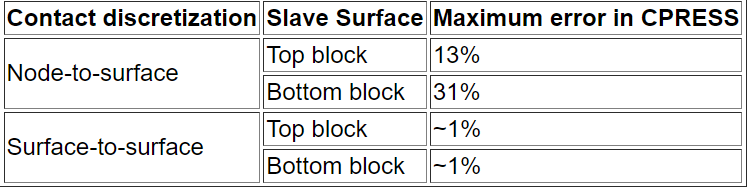
分别使用点面接触与面面接触的接触应力计算结果误差如下所示,可以看到使用面面接触计算误差更小
3.主从面确定
从个人经验,主从面的确定原则为:
面积较大的面作为主面
面积相近,刚度较大的面做主面(这里的刚度还包括结构刚度)
刚度相近,网格划分较细的面作为从面(避免主面穿透从面的情况出现)
持续更新中,欢迎大家关注、追更




















